2.1. Однородные дифференциальные уравнения
Если общее решение дифференциального уравнения представлено в виде квадратур (интегралов) от элементарных функций и функций, входящих в состав дифференциального уравнения, то говорят, что Уравнение проинтегрировано в квадратурах.
Функция ![]() называется Однородной функцией степени
называется Однородной функцией степени ![]() Относительно переменных
Относительно переменных ![]() и
и ![]() в смысле Эйлера, если при любом допустимом
в смысле Эйлера, если при любом допустимом ![]() справедливо тождество
справедливо тождество
![]() .
.
Если ![]() , то функция
, то функция ![]() называется Однородной функцией нулевой степени. Для функции
называется Однородной функцией нулевой степени. Для функции ![]() имеем
имеем
![]() ,
,
Так что это однородная функция нулевой степени.
Дифференциальное уравнение вида ![]() называется Однородным Дифференциальным уравнением, если
называется Однородным Дифференциальным уравнением, если ![]() есть однородная функция нулевой степени относительно
есть однородная функция нулевой степени относительно ![]() и
и ![]() .
.
В этом случае можно положить ![]() . Тогда в силу однородности функции
. Тогда в силу однородности функции ![]() и
и ![]() , то есть однородное дифференциальное уравнение примет вид
, то есть однородное дифференциальное уравнение примет вид
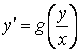 . (2.1)
. (2.1)
Сделаем замену переменной ![]() , откуда
, откуда ![]() . Тогда
. Тогда ![]() и для уравнения (2.1) имеем
и для уравнения (2.1) имеем
![]() . (2.2)
. (2.2)
Преобразуем это уравнение с разделяющимися переменными:
![]() ,
, ![]() ,
, 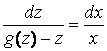 .
.
Получено дифференциальное уравнение с разделенными переменными. Интегрируя последнее равенство, имеем

Пусть ![]() – первообразная подынтегральной функции левой части. Тогда
– первообразная подынтегральной функции левой части. Тогда ![]() – интеграл дифференциального уравнения (2.2). Следовательно, решение исходного однородного дифференциального уравнения (2.1)
– интеграл дифференциального уравнения (2.2). Следовательно, решение исходного однородного дифференциального уравнения (2.1)
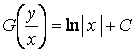 .
.
Таким образом, замена переменной ![]() всегда приводит однородное дифференциальное уравнение (2.1) к уравнению с разделяющимися переменными (2.1).
всегда приводит однородное дифференциальное уравнение (2.1) к уравнению с разделяющимися переменными (2.1).
Пример 2.1. Решить дифференциальное уравнение
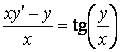 .
.
Решение. Перепишем это уравнение в виде
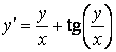 .
.
Полагая в нем ![]() , учитывая, что
, учитывая, что ![]() и
и ![]() , получим:
, получим:
![]() ,
, ![]() ,
, ![]() .
.
Интегрируя последнее уравнение, имеем:
![]() ,
, ![]() ,
, ![]() .
.
Окончательно
![]() .
.
| < Предыдущая | Следующая > |
|---|