1.4. Уравнения с разделяющимися переменными

Дифференциальным уравнением с разделяющимися переменными называется уравнение первого порядка вида (1.5), где

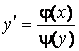. (1.8)

В этом случае

,

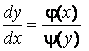Откуда

.

Такое уравнение называется Уравнением с разделенными переменными. Возьмем неопределенный интеграл от обеих частей этого уравнения

.

Пусть и – первообразные функций и . Тогда

,

Где – произвольная постоянная. Таким образом, решение уравнения (1.8) находится с точностью до произвольной постоянной .

Пример 1.1. Решить дифференциальное уравнение

. (1.9)

Решение. Перепишем это уравнение, выражая производную через дифференциалы

.

Разделим переменные

.

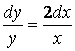Возьмем несобственные интегралы от обеих частей

.

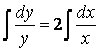Имеем

.

Потенцируя это равенство, окончательно имеем

.

Таким образом, уравнению (1.9) удовлетворяет бесчисленное множество парабол.

Кроме представленной формы (1.8) уравнения с разделяющимися переменными могут быть записаны и в дифференциальной форме

.

Отсюда получим, что

,

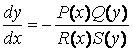Или

,

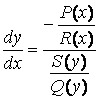Что приводит к виду (1.8) при

, .

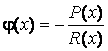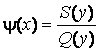Большинство интегрируемых дифференциальных уравнений первого порядка путём алгебраических преобразований приводятся к уравнениям с разделяющимися переменными. Этот тип уравнений является базовым.

Рассмотрим пример замены переменных, приводящий к уравнению вида (1.8). Пусть дано дифференциальное уравнение

, (1.10)

Где , и – некоторые числа. Введем переменную . Дифференцируя это равенство по переменной , имеем , откуда

.

Исключая и из исходного уравнения (1.10), имеем

,

Откуда

. (1.11)

Правая часть этого уравнения зависит только от , значит это уравнение с разделяющимися переменными. Его решение сводится к преобразованиям:

, , .

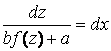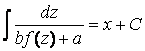Обозначим первообразную функции через . Тогда интеграл дифференциального уравнения с разделяющимися переменными (1.11) имеет вид

.

Переходя к исходным переменным, имеем решение исходного уравнения (1.10)

.

< Предыдущая		Следующая >