1.3. Уравнения первого порядка и их геометрический смысл

Дифференциальное уравнение первого порядка может быть записано в общем виде, аналогичному уравнению -го порядка (1.3):

. (1.4)

Если это уравнение разрешить относительно производной, то

. (1.5)

Простейший пример такого уравнения

, (1.6)

Из которого неизвестная функция находится интегрированием

,

Где слева стоит неопределенный интеграл. Если функция имеет первообразную , то .

В этом простейшем случае решение содержит произвольную постоянную , которая может быть определена, если задать Начальное условие

или , (1.7)

Где и – некоторые числа, то есть при некотором значении независимой переменной заранее задано значение искомой функции .

Геометрически начальное условие (1.7) означает, что на плоскости задана точка , через которую должна проходить искомая интегральная кривая. При таком начальном условии решение уравнения (1.6) можно представить в виде

.

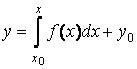Рассмотрим уравнение (1.5). Пусть – область определения функции на плоскости . Возьмём некоторую точку и вычислим значение функции в ней . В соответствии с исходным дифференциальным уравнением получим значение производной неизвестной функции в заданной точке, то есть . Поскольку производная функций определяет угловой коэффициент наклона касательной к графику функции, то тем самым определим угловой коэффициент касательной к той интегральной кривой уравнения, которая проходит через точку .

Возьмем теперь другую точку и вычислим для нее величину . Это есть коэффициент наклона касательной к интегральной кривой, проходящей через эту новую точку. Точно так же, беря новые точки в области , получим множество элементарных «кусочков» интегральных кривых этого уравнения, проходящих через взятые точки.

Геометрический смысл дифференциального уравнения (1.5) заключается в том, что оно устанавливает зависимость между координатами точек интегральной кривой и значением производной , то есть в каждой точке определяется направление касательной к искомой интегральной кривой. Таким образом, уравнение (1.5) определяет поле направлений, и задача интегрирования дифференциального уравнения заключается в том, чтобы найти кривые, направления касательных к которым в каждой точке совпадают с направлением поля. Каждая из интегральных кривых представляет собой график решения исходного дифференциального уравнения. Найти решение уравнения с начальным условием (1.7) геометрически означает выделение из множества интегральных кривых той кривой, которая проходит через точку . Всё множество интегральных кривых представляет общее решение дифференциального уравнения. При графическом представлении решения дифференциального уравнения часто пользуются изоклинами.

Изоклиной Называется геометрическое место точек, для которых производная некоторой функции имеет одно и то же значение. Уравнение изоклины имеет вид . Для дифференциального уравнения (1.5) изоклины представляются равенством . Графический метод решения дифференциального уравнения с помощью изоклин используется в том случае, когда аналитическое решение невозможно.

< Предыдущая		Следующая >