11.2. ИДЗ–2. Производные и дифференциалы высших порядков
1 Вычислить значение второй производной функции ![]() в точке
в точке ![]() .
.
1.1 ![]() .
.
1.2 ![]() .
.
1.3 ![]() .
.
1.4 ![]() .
.
1.5 ![]() .
.
1.6 ![]() .
.
1.7 ![]() .
.
1.8 ![]() .
.
1.9 ![]() .
.
1.10 ![]() .
.
1.11 ![]() .
.
1.12 ![]() .
.
1.13 ![]() .
.
1.14 ![]() .
.
1.15 ![]() .
.
1.16 ![]() .
.
1.17 ![]() .
.
1.18 ![]() .
.
1.19 ![]() .
.
1.20. ![]() .
.
1.21 ![]() .
.
1.22 ![]() .
.
1.23 ![]() .
.
1.24 ![]() .
.
1.25 ![]() .
.
1.26 ![]() .
.
1.27 ![]() .
.
1.28 ![]() .
.
1.29 ![]() .
.
1.30 ![]() .
.
2 Разложить функцию ![]() в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки ![]() :
:
2.1 ![]() . 2.2
. 2.2 ![]() .
.
2.3 ![]() . 2.4
. 2.4 ![]() .
.
2.5 ![]() . 2.6
. 2.6 ![]() .
.
2.7 ![]() . 2.8
. 2.8 ![]() .
.
2.9 ![]() . 2.10
. 2.10 ![]() .
.
2.11 ![]() . 2.12
. 2.12 ![]() .
.
2.13 ![]() . 2.14
. 2.14 ![]() .
.
2.15 ![]() . 2.16
. 2.16 ![]() .
.
2.17 ![]() . 2.18
. 2.18 ![]() .
.
2.19 ![]() в точке
в точке ![]() . 2.20
. 2.20 ![]() в точке
в точке ![]() .
.
2.21 ![]() . 2.22
. 2.22 ![]() .
.
2.23 ![]() . 2.24
. 2.24 ![]() .
.
2.25 ![]() . 2.26
. 2.26 ![]() в точке
в точке ![]() .
.
2.27 ![]() . 2.28.
. 2.28. ![]() .
.
2.29 ![]() . 2.30
. 2.30 ![]() .
.
3 Написать разложение функции ![]() В ряд Маклорена по степеням переменной
В ряд Маклорена по степеням переменной ![]() до членов порядка
до членов порядка ![]() включительно:
включительно:
3.1 ![]()
![]() . 3.2
. 3.2 ![]()
![]() .
.
3.3 ![]()
![]() 3.4
3.4 ![]()
![]() .
.
3.5 ![]()
![]() . 3.6
. 3.6 ![]()
![]() .
.
3.7 ![]()
![]() . 3.8
. 3.8 ![]()
![]() .
.
3.9 ![]()
![]() . 3.10
. 3.10 ![]()
![]() .
.
3.11 ![]()
![]() . 3.12
. 3.12 ![]()
![]() .
.
3.13 ![]()
![]() . 3.14
. 3.14 ![]()
![]() .
.
3.15 ![]()
![]() . 3.16
. 3.16 ![]()
![]() .
.
3.17 ![]()
![]() . 3.18
. 3.18 ![]()
![]() .
.
3.19 ![]()
![]() . 3.20
. 3.20 ![]()
![]() .
.
3.21 ![]()
![]() . 3.22
. 3.22 ![]()
![]() .
.
3.23 ![]()
![]() . 3.24
. 3.24 ![]()
![]() .
.
3.25 ![]()
![]() . 3.26
. 3.26 ![]()
![]() .
.
3.27 ![]()
![]() . 3.28
. 3.28 ![]()
![]() .
.
3.29 ![]()
![]() . 3.30
. 3.30 ![]()
![]() .
.
4 Используя правило Лопиталя, вычислить пределы:
4.1 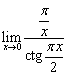 . 4.2
. 4.2 ![]() .
.
4.3  . 4.4
. 4.4 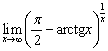
4.5 ![]() . 4.6
. 4.6 ![]() .
.
4.7 ![]() . 4.8
. 4.8 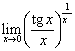 .
.
4.9 ![]() . 4.10
. 4.10 ![]() .
.
4.11 ![]() . 4.12
. 4.12 ![]() .
.
4.13 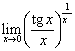 4.14
4.14 ![]()
4.15 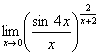 4.16
4.16 ![]() .
.
4.17 ![]() . 4.18
. 4.18 ![]() .
.
4.19 ![]() . 4.20
. 4.20 ![]() .
.
4.21 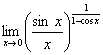 4.22
4.22 ![]() .
.
4.23 ![]() . 4.24
. 4.24 ![]() .
.
4.25 ![]() . 4.26
. 4.26 ![]() .
.
4.27 ![]() . 4.28
. 4.28 ![]() .
.
4.29 ![]() . 4.30
. 4.30 ![]() .
.
5 Вычислить приближенно значение функции ![]() в точке
в точке ![]() с помощью дифференциала:
с помощью дифференциала:
5.1 ![]() ,
, ![]() 7,76.
7,76.
5.2 ![]() ,
, ![]() 0.98.
0.98.
5.3 ![]() ,
, ![]() 0,08.
0,08.
5.4 ![]() ,
, ![]() 2,01.
2,01.
5.5 ![]() ,
, ![]()
![]() .
.
5.6 ![]() ,
, ![]() 1,08.
1,08.
5.7 ![]() ,
, ![]() 0,01.
0,01.
5.8 ![]() ,
, ![]() 0,48.
0,48.
5.9 ![]() ,
, ![]() 1,03.
1,03.
5.10 ![]() ,
, ![]() 1,95.
1,95.
5.11 ![]() ,
, ![]() 0,51.
0,51.
5.12 ![]() ,
, ![]() 1,012.
1,012.
5.13 ![]() ,
, ![]() 2,002.
2,002.
5.14 ![]() ,
, ![]() 0,52.
0,52.
5.15![]() ,
, ![]() 8,24.
8,24.
5.16 ![]() ,
, ![]() 10,02.
10,02.
5.17 ![]() ,
, ![]()
![]() .
.
5.18 ![]() ,
, ![]() 0,01.
0,01.
5.19 ![]() ,
, ![]() 0,98.
0,98.
5.20 ![]() ,
, ![]() 3,998.
3,998.
5.21 ![]() ,
, ![]() 1,04
1,04
5.22 ![]() ,
, ![]() 1,21.
1,21.
5.23 ![]() ,
, ![]() 4,16.
4,16.
5.24 ![]() ,
, ![]() 1,02.
1,02.
5.25 ![]() ,
, ![]() 2,56.
2,56.
5.26 ![]() ,
, ![]() 2,995.
2,995.
5.27 ![]() ,
, ![]() 0,09
0,09
5.28 ![]() ,
, ![]()
![]() .
.
5.29 ![]() ,
, ![]() 7,64.
7,64.
5.30 ![]() ,
, ![]() 1,95.
1,95.
| < Предыдущая | Следующая > |
|---|