10.4. Эволюта и эвольвента плоской кривой

Из определения центра кривизны следует, что каждой точке кривой , соответствует точка – центр кривизны кривой в точке .

Множество точек центров кривизны линии называется ее эволютой, а сама линия по отношению к своей эволюте называется эвольвентой.

Пусть кривая задана уравнением в плоскости . Пусть – центр кривизны линии в точке (рисунок 10.4).

Тогда для любой точки имеем . Обозначим

, , ,

Где – единичный вектор нормали кривой .

Тогда

.

Это уравнение называется векторным уравнением эволюты кривой .

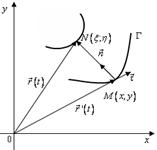
Рисунок 10.4 – Эволюта и эвольвента

Запишем разложения векторов и по базису :

,

.

Найдем вектор .

Единичный вектор касательной к кривой есть

.

Продифференцируем равенство по . Имеем

.

Отсюда . Таким образом, вектор нормали .

Координаты вектора :

.

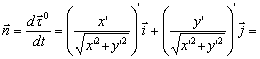
Тогда

.

Подставим и в векторное уравнение эволюты :

.

Приравнивая коэффициенты при и в левой и правой частях выражения, получим:

,

.

Данные формулы являются параметрическими уравнениями эволюты кривой . Сама же кривая является эвольвентой по отношению к кривой .

Свойства эволюты и эвольвенты, устанавливающие связь между ними:

– нормаль к эвольвенте является касательной к эволюте в соответствующей точке;

– если на некотором участке эвольвенты радиус кривизны изменяется монотонно, то приращение радиуса кривизны на этом участке равно по абсолютной величине длине дуги соответствующего участка эволюты.

Вопросы для самоконтроля

1 Дайте определение кривизны и радиуса кривизны кривой.

2 Как вычисляется кривизна в случаях векторного, параметрического представления кривой?

3 Дайте определение радиуса, круга и центра кривизны плоской кривой.

4 Что называется эволютой и эвольвентой плоской кривой?

< Предыдущая		Следующая >