10.3. Радиус, круг и координаты центра кривизны плоской кривой

Проведем к кривой нормаль в точке и отложим на этой нормали в сторону вогнутости кривой отрезок (рисунок 10.3), по величине обратный кривизне : .

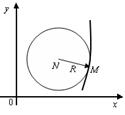
Рисунок 10.3 – Радиус кривизны MN

Отрезок называется радиусом кривизны, точка – центром кривизны, а круг с центром в точке и радиусом – кругом кривизны кривой в точке .

Если кривая задана в декартовой системе координат уравнением , то ее радиус кривизны находится по формуле:

.

Если кривая в плоскости задана параметрическими уравнениями, то ее радиус кривизны определяется по формуле:

.

Если – годограф вектор-функции , то:

.

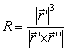< Предыдущая		Следующая >