10.2. Вычисление кривизны кривой

Пусть кривая является годографом дважды дифференцируемой векторной функции действительного аргумента (рисунок 10.3).

Тогда кривизна кривой вычисляется по формуле

.

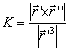Если гладкая кривая задана параметрическими уравнениями

,

То кривизна вычисляется по формуле

.

Если кривая задана в плоскости уравнением , то формула для вычисления ее кривизны получается из формулы вычисления кривизны, положив в ней , . Тогда уравнение линии можно записать в параметрическом виде:

Отсюда

и .

Значит,

.

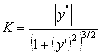Если кривая задана в плоскости неявно уравнением , то кривизна вычисляется по формуле

.

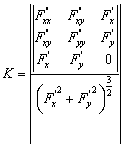Если кривая задана в плоскости в полярных координатах уравнением , то кривизна находится по формуле

.

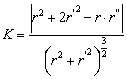< Предыдущая		Следующая >