10.1. Понятие кривизны кривой

Одной из важных характеристик кривой является мера ее изогнутости – кривизна.

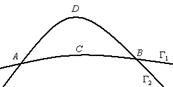
Например, о двух плоских кривых и (рисунок 10.1) можно сказать, что кривая более изогнута, чем .

Рисунок 10.1 – Кривые и	Рисунок 10.2 – Угол смежности

Однако для того, чтобы строго оценить степень изогнутости плоской линии, необходимо ввести количественную характеристику ее изогнутости (кривизны).

Рассмотрим на кривой точки и . Проведем в этих точках касательные к кривой. При переходе по кривой из точки в точку касательная поворачивается на угол , который называется углом смежности (рисунок 10.2).

Отношение угла смежности дуги к ее длине называется средней кривизной дуги: .

Средняя кривизна характеризует среднюю изогнутость кривой на всей дуге. На отдельных участках кривой кривизна может значительно отличаться от средней. Чтобы избежать такой неопределенности, вводится количественная мера изогнутости кривой в точке . Эта характеристика основана на том, что чем меньше дуга (рисунок 10.2), тем лучше средняя кривизна характеризует изогнутость линии вблизи точки .

Кривизной линии в точке называется предел, к которому стремится средняя кривизна дуги линии при стремлении точки к точке :

.

< Предыдущая		Следующая >