10.5. Решение типовых примеров

1 Вычислить кривизну кривой в точке .

Решение. Находим,. Тогда кривизна кривой в любой ее точке с абсциссой есть

.

В точке имеем

.

2 Найти кривизну в любой точке циклоиды

Решение. Имеем

, ,

, .

Тогда

,

.

Подставляя в формулу для вычисления кривизны, получим

.

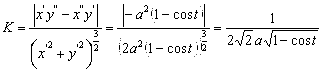3 Найти координаты центра кривизны кривой в точке .

Решение. Дифференцируем уравнение два раза:

, .

Так как , , то из первого выражения находим, что , а из второго получаем .

Подставляя в формулы для координат центра кривизны, получим

,

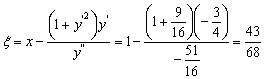, т. е. .

4 Найти эволюту эллипса .

Решение. Имеем

, , , .

Подставляя в формулы для эволюты, получим

, .

Данные уравнения являются параметрическими уравнениями астроиды (рисунок 10.6).

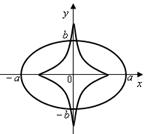
Рисунок 10.6 – Эллипс и его эволюта

5 Составить уравнение эволюты параболы

.

Решение. Продифференцируем два раза уравнение параболы:

, ,

, .

Определяем координаты центра кривизны:

,

.

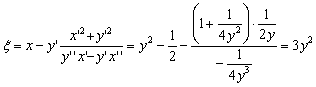Получаем уравнение эволюты в параметрической форме:

, .

Исключив параметр , найдем уравнение эволюты в явном виде

.

< Предыдущая		Следующая >