09.5. Решение типовых примеров
1 Найти годограф вектор-функции
.
Решение. Параметрические уравнения годографа есть
, 
, 
.
Из первых двух уравнений исключаем параметр 
:
.
Следовательно, годографом вектор-функции является окружность
, 
,
Из которой исключена точка 
.
При изменении от 
до 
точка 
на годографе движется от точки против часовой стрелки (если наблюдать из точки, расположенной выше плоскости ). При этом
, 
.
2 Вычислить 
, если 
.
Решение. Согласно определению
.
3 Найти единичный касательный вектор годографа вектор-функции
При 
.
Решение. Параметрические уравнения годографа есть
, 
, 
.
Найдем координаты направляющего вектора касательной к кривой 
:
,
В частности в точке
.
Тогда единичный вектор годографа имеет вид
.
4 Найти производную скалярного произведения векторов
и 
.
Решение. Согласно свойствам дифференцируемых векторных функций, имеем
=
=
.
5 Дано уравнение движения 
. Определить траекторию и скорость движения.
Решение. Параметрические уравнения годографа есть
, 
, .
Из первого уравнения исключим параметр
И подставим во второе
.
Отсюда уравнение траектории движения
, 
.
Вектор скорости движения есть
.
6 Написать уравнения касательной и нормальной плоскости к кривой
В точке 
.
Решение. Данной точке соответствует значение параметра 
.
Имеем
, 
, 
.
Подставляя значение , получаем
, 
, 
.
Тогда уравнение касательной:
,
Уравнение нормальной плоскости:
Или 
.
7 Найти скорость и ускорение материальной точки 
, движущейся с постоянной угловой скоростью 
по окружности
.
Решение. Пусть – произвольная точка окружности. Обозначим через 
угол между радиус-вектором точки и положительным направлением оси 
. По условию
,
Где – время движения.
Выразим координаты точки как функции времени (рисунок 9.8):
,
.
Следовательно, радиус-вектор точки
,
Скорость 
движения точки
,
Модуль скорости
.
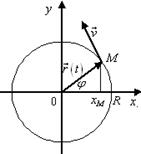
Рисунок 9.8 – Геометрическая интерпретация задачи 7.
Скалярное произведение векторов 
и 
есть:
,
Т. е. векторы и перпендикулярны.
Отсюда следует, что вектор направлен по касательной к окружности, по которой движется точка .
Найдем ускорение 
:
.
Значит, векторы 
и имеют противоположные направления.
Таким образом, ускорение материальной точки, движущейся с постоянной угловой скоростью по окружности, в каждый момент времени направлено к центру этой окружности.
8 К годографу винтовой линии (рисунок 9.9)
А) найти уравнения касательной прямой и нормальной плоскости в точке 
;
Б) доказать, что касательная к винтовой линии образует постоянный угол с осью 
;
В) записать натуральное уравнение винтовой линии;
Г) найти дифференциал длины дуги.
Рисунок 9.9 – Годограф функции
Решение. а) координаты точки касания 
есть:
, 
, 
.
Координаты вектора 
:
, 
. 
.
Тогда уравнение касательной прямой имеет вид
,
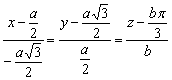А уравнение нормальной плоскости
;
Б) вектор касательный к годографу вектора :
.
Тогда
.
В) векторная функция 
является непрерывно дифференцируемой и
.
Тогда 
. Интегрируя обе части, получим 
. Из начального условия 
, имеем 
. При этом длина винтовой линии равна
.
Следовательно, 
.
Отсюда натуральное уравнение винтовой линии в координатной форме запишется в виде:
,
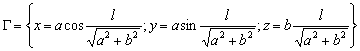Где 
.
Г) дифференциал длины дуги равен
.
Для винтовой линии имеем
.
| < Предыдущая | Следующая > |
|---|
