09.4. Натуральное уравнение гладкой кривой и уравнение нормальной плоскости
Пусть кривая ![]() гладкая кривая. В силу теоремы 2 переменная длина дуги
гладкая кривая. В силу теоремы 2 переменная длина дуги ![]() , отсчитываемая от начала
, отсчитываемая от начала ![]() кривой
кривой ![]() , является строго возрастающей непрерывно дифференцируемой функцией с производной, положительной во всех точках отрезка
, является строго возрастающей непрерывно дифференцируемой функцией с производной, положительной во всех точках отрезка ![]() :
: ![]() . Так как
. Так как ![]() и
и ![]() , то обратная функция
, то обратная функция ![]() однозначна, строго возрастает, непрерывно дифференцируема на отрезке
однозначна, строго возрастает, непрерывно дифференцируема на отрезке ![]() . По теореме об обратной функции имеем
. По теореме об обратной функции имеем
![]() .
.
Таким образом, для всякой гладкой кривой ![]() ее параметр
ее параметр ![]() является строго возрастающей непрерывно дифференцируемой функцией переменной длины
является строго возрастающей непрерывно дифференцируемой функцией переменной длины ![]() , производная этой функции нигде не обращается в нуль.
, производная этой функции нигде не обращается в нуль.
Следовательно, функция ![]() является допустимым преобразованием параметра и уравнение кривой
является допустимым преобразованием параметра и уравнение кривой ![]() можно записать в виде
можно записать в виде ![]() ,
, ![]() .
.
Если параметром кривой ![]() является переменная длина ее дуги
является переменная длина ее дуги ![]() , то
, то ![]() называется натуральным параметром, а уравнение кривой
называется натуральным параметром, а уравнение кривой ![]() называется натуральным уравнением кривой.
называется натуральным уравнением кривой.
Теорема 3 Пусть кривая ![]() гладкая, a
гладкая, a ![]() – переменная длина ее дуги. Тогда
– переменная длина ее дуги. Тогда ![]() является единичным касательным к кривой
является единичным касательным к кривой ![]() вектором и
вектором и ![]() .
.
Из теоремы 3 следует, что если ![]() ,
, ![]() ,
, ![]() – углы, образованные вектором касательной
– углы, образованные вектором касательной ![]() к кривой
к кривой ![]() С осями
С осями ![]() ,
, ![]() ,
, ![]() соответственно, то
соответственно, то![]() .
.
Нормальной плоскостью к кривой ![]() называется плоскость, перпендикулярная касательной прямой и проходящая через точку касания.
называется плоскость, перпендикулярная касательной прямой и проходящая через точку касания.
Пусть ![]() – точка касания (рисунок 9.7). Из аналитической геометрии известно, что уравнение плоскости
– точка касания (рисунок 9.7). Из аналитической геометрии известно, что уравнение плоскости ![]() , проходящей через эту точку, имеет вид
, проходящей через эту точку, имеет вид
![]() ,
,
Где ![]() – нормальный вектор плоскости.
– нормальный вектор плоскости.
Из определения нормальной плоскости следует, что векторы ![]() и
и ![]() коллинеарные, поэтому можно положить
коллинеарные, поэтому можно положить ![]() ,
, ![]() ,
, ![]() . Тогда искомое уравнение плоскости будет иметь вид:
. Тогда искомое уравнение плоскости будет иметь вид:
![]() .
.
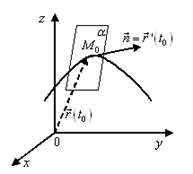
Рисунок 9.7 – Нормальная плоскость ![]() к кривой
к кривой ![]()
Вопросы для самоконтроля
1 Дайте определение векторной функции и годографа.
2 Дайте определение предела и непрерывности векторной функции. Перечислите свойства предела вектор-функции.
3 Дайте определение производной векторной функции. Какая вектор-функция называется дифференцируемой? Что называется дифференциалом векторной функции?
4 В чем состоит геометрический и физический смысл производной вектор-функции?
5 Дайте определение кривой. Перечислите способы задания кривой.
6 Какая прямая называется касательной к кривой?
7 Какая кривая называется гладкой кривой?
8 Что называется разбиением кривой?
9 Какая кривая называется спрямляемой? Дайте определение длины кривой.
10 Чему равен дифференциал дуги?
11 Какое уравнение называется натуральным уравнением гладкой кривой?
12 Чему равна длина единичного вектора касательной? Какие координаты он имеет?
| < Предыдущая | Следующая > |
|---|