09.3. Длина кривой

Пусть в трехмерном пространстве задана прямоугольная система координат . И пусть на отрезке заданы непрерывные функции , , . Тогда говорят, что задано непрерывное отображение отрезка в .

Числа , , можно рассматривать как координаты точки или как координаты радиус-вектора с началом в точке и концом в точке (рисунок 9.6):

, .

Непрерывное отображение отрезка в пространство называется кривой и обозначается .

Множество точек пространства , на которое отображается отрезок , называется носителем кривой , переменная называется параметром на кривой .

Если носитель кривой лежит в некоторой плоскости, то эта кривая называется плоской.

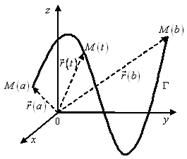
Рисунок 9.6 – Кривая в пространстве

Кривая может быть задана:

– явно: непрерывная функция , , задает плоскую кривую , носителем является график функции , параметром – переменная ;

– неявно: координаты всех точек носителя плоской кривой удовлетворяют уравнению ;

– в координатной форме: , где , , координатные функции отображения , ;

– векторное представление: , где – вектор-функция.

Если для точек кривой выполняется условие предшествует , то такая кривая называется ориентированной.

Точка носителя кривой, в которую при отображении отображаются хотя бы две разные точки отрезка , называется точкой самопересечения (кратной точкой) кривой .

Если носитель кривой не имеет кратных точек (отображение взаимно однозначно отображает отрезок в точки пространства ), то кривая называется простой дугой.

Если и , то точка называется началом кривой , а точка – концом данной кривой. Если , то кривая называется замкнутой.

Простым замкнутым контуром называется замкнутая кривая, у носителя которой нет кратных точек, кроме носителя ее начала и конца.

Если , , то кривая называется частью кривой или простой дугой с началом в точке и концом в точке .

Прямая проходящая через точку в направлении вектора , называется касательной к кривой в точке .

Поместим начало вектора в точку . Направление данного вектора совпадает с направлением касательной. Поэтому уравнение касательной в векторной форме запишется в виде

, ,

Где – радиус-вектор касательной.

В координатной форме уравнение примет вид

,

,

,

Где .

Выражая параметр , получим уравнение касательной в канонической форме:

.

Если функция непрерывна на отрезке , то кривая называется непрерывно дифференцируемой кривой. Если векторная функция раз дифференцируема на отрезке , то кривая называется раз дифференцируемой кривой.

Точка кривой , в которой , называется неособой, а точка, в которой – особой.

Пусть . Тогда . Поэтому точка является неособой точкой кривой тогда и только тогда, когда

.

Из определения неособой точки следует, что во всякой неособой точке кривой Г существует касательная.

Гладкой кривой называется кривая, которая является непрерывно дифференцируемой и не имеет особых точек. Если кривая составлена из конечного числа гладких кривых, то такая кривая называется кусочно-гладкой.

Для отрезка система , , точек , таких, что , называется разбиением отрезка . Соответствующий набор точек , , где называется разбиением кривой .

Соединив последовательно точки , , , , отрезками , , , получим ломаную , которая называется вписанной в кривую ; отрезки , называются звеньями ломаной , а точки ломаной – вершинами ломаной. Длина каждого отрезка равна . Тогда длина всей ломаной равна

.

Верхняя грань длин всевозможных ломаных, вписанных в данную кривую, называется длиной кривой:

,

Где верхняя грань берется по всевозможным разбиениям , , отрезка .

Если , то кривая Г называется спрямляемой.

Теорема 2 Если кривая непрерывно дифференцируема, то переменная длина дуги , отсчитываемая от начала кривой , является возрастающей непрерывно дифференцируемой функцией параметра и

.

Поскольку , то отсюда дифференциал длины дуги равен

.

< Предыдущая		Следующая >