06.4. Решение типовых примеров

1 Найти интервалы монотонности и точки экстремума функции .

Решение. Областью определения данной функции является множество .

Производная этой функции имеет вид

И обращается в нуль в точке . При этом производная не существует в точках и . Поэтому точками возможного экстремума являются , , . Они разбивают область определения на четыре интервала монотонности: , , , .

Видно, что при , при . Следовательно, функция монотонно возрастает при , и монотонно убывает при . Согласно первому достаточному условию локального экстремума, в точке функция достигает максимума, , а в точке функция имеет минимум, .

2 Найти экстремумы функции .

Решение. Данная функция определена при всех . Производная данной функции имеет вид

Производная не обращается в нуль ни при каких значениях и не существует при . Поэтому точка является точкой возможного экстремума функции.

При имеем , при имеем . Согласно первому достаточному условию точка является точкой максимума, .

3 Найти экстремумы функции .

Решение. Данная функция определена при .

Найдем первую производную

Решая уравнение , найдем

, .

При этом функция не существует при .

Значит, точками возможного экстремума являются , , , . В точках экстремума нет, так как по определению производной точками экстремума могут быть лишь внутренние точки области определения.

Вторая производная функции имеет вид

Так как , то функция имеет в точке минимум, и

В точке получим .

Значит в точке функция имеет максимум, и

4 Найти на отрезке глобальные экстремумы функции

Решение. Определяем точки возможного экстремума (стационарные точки) функции :

, .

Значит, и .

Так как при имеем , при имеем , то является точкой максимума. Так как при имеем и при имеем , то является точкой минимума.

Вычисляем значения на концах отрезка и в стационарных точках, принадлежащих отрезку:

, , , .

Тогда

Наименьшее значение данная функция принимает на левом конце отрезка в точке , наибольшее – в точке и на правом конце отрезка в точке . График данной функции изображен на рисунке 6.4.

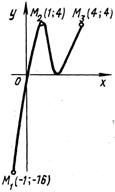
Рисунок 6.4 – График функции

На отрезке

5 Баржу, палуба которой на М ниже уровня пристани, подтягивают к ней при помощи каната, наматываемого на ворот, со скоростью м/с. С каким ускорением движется баржа в момент, когда она удалена от пристани на расстояние L=8м (по горизонтали)?

Решение. Пусть через T секунд после начала движения баржа (рисунок 6.5) находится на расстоянии м от пристани (по горизонтали).

Рисунок 6.5 – Геометрическая интерпретация задачи 5

Тогда длина каната представляет собой функцию

Производная которой имеет вид

Поскольку канат подтягивают, то по условию задачи .

Отсюда

Разрешая относительно , получим скорость движения баржи

Ускорение движения баржи есть вторая производная от функции :

Если – тот момент времени, когда =8, то

(м/с2).

6 Боковая сторона равнобедренной трапеции равна ее меньшему основанию. Каков должен быть угол при большем основании, чтобы площадь трапеции была наибольшей?

Решение. На рисунке 6.6 изображена трапеция . Пусть . Тогда по условию . Пусть BE И CF – высоты трапеции; BE=CF. Полагая ÐBAD=A, выразим площадь трапеции как функцию от :