06.2. Необходимое и достаточные условия существования локального экстремума функции
Теорема 2 (необходимое условие экстремума) Если в точке ![]() функция
функция ![]() достигает экстремума, то ее производная в этой точке равна нулю или не существует.
достигает экстремума, то ее производная в этой точке равна нулю или не существует.
Из теоремы 2 следует, что в точках экстремума функции ![]() касательная к ее графику:
касательная к ее графику:
– параллельна оси абсцисс, если существует ![]() (рисунок 6.2, а);
(рисунок 6.2, а);
– параллельна оси ординат, если ![]() бесконечна (рисунок 6.2, б);
бесконечна (рисунок 6.2, б);
– существуют не совпадающие левая и правая касательные, если ![]() (рисунок 6.2,в).
(рисунок 6.2,в).
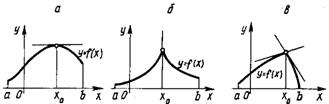
Рисунок 6.2 – Положение касательной к графику
Функции в точках экстремума
Точки, в которых производная функции ![]() обращается в нуль или не существует, называют Критическими или Точками возможного экстремума. Точки, в которых производная функции
обращается в нуль или не существует, называют Критическими или Точками возможного экстремума. Точки, в которых производная функции ![]() обращается в нуль, называют Стационарными.
обращается в нуль, называют Стационарными.
Критическая точка ![]() называется Угловой точкой Функции
называется Угловой точкой Функции ![]() если
если ![]() (рисунок 6.2, в). Критическая точка
(рисунок 6.2, в). Критическая точка ![]() называется Точкой Возврата функции, если ее левая
называется Точкой Возврата функции, если ее левая ![]() и правая
и правая ![]() производные бесконечны (рисунок 6.2, б).
производные бесконечны (рисунок 6.2, б).
Не всякая критическая точка функции ![]() является точкой ее локального экстремума.
является точкой ее локального экстремума.
Теорема 3 (первый достаточный признак существования экстремума функции) Пусть ![]() – критическая точка непрерывной функции
– критическая точка непрерывной функции ![]() . Если
. Если ![]() при переходе через точку
при переходе через точку ![]() меняет знак с «+» на «–», то
меняет знак с «+» на «–», то ![]() – точка локального максимума; если
– точка локального максимума; если ![]() при переходе через точку
при переходе через точку ![]() меняет знак с «–» на «+», то
меняет знак с «–» на «+», то ![]() – точка локального минимума; если
– точка локального минимума; если ![]() при переходе через точку
при переходе через точку ![]() не меняет знак, то
не меняет знак, то ![]() не является точкой локального экстремума.
не является точкой локального экстремума.
Теорема 4 (второй достаточный признак существования экстремума функции) Стационарная точка ![]() функции
функции ![]() , дважды дифференцируемой в
, дважды дифференцируемой в ![]() , является точкой локального минимума
, является точкой локального минимума ![]() , если
, если ![]() , и точкой локального максимума, если
, и точкой локального максимума, если ![]() (рисунок 6.3).
(рисунок 6.3).
|
а)
|
Б)
|
|
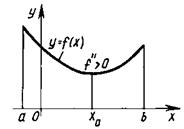
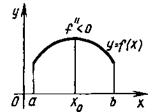
Рисунок 6.3 – Локальные минимум (а) и максимум (б) функции |
Теорема 5 (третий достаточный признак существования экстремума функции) Пусть функция ![]() –
– ![]() раз непрерывно дифференцируема в точке
раз непрерывно дифференцируема в точке ![]() и в этой точке
и в этой точке
![]() ,
, ![]() .
.
Тогда:
1) если ![]() – четное и
– четное и ![]() , то
, то ![]() – точка локального максимума.
– точка локального максимума.
2) если ![]() – четное и
– четное и ![]() , то
, то ![]() – точка локального минимума;
– точка локального минимума;
3) если ![]() – нечетное, то
– нечетное, то ![]() не является точкой локального экстремума.
не является точкой локального экстремума.
| < Предыдущая | Следующая > |
|---|