06.1. Точки локального и глобального экстремума

С помощью производной функции можно произвести полное исследование функции (найти промежутки возрастания и убывания, экстремумы, точки перегиба, промежутки выпуклости и вогнутости, асимптоты графика) и построить график этой функции.

Теорема 1 Для того чтобы дифференцируемая на функция не убывала (не возрастала) на этом интервале, необходимо и достаточно, чтобы () для всех . Если же для любого (), то функция возрастает (убывает) на этом интервале.

Геометрический смысл теоремы. Касательная к графику возрастающей на функции () составляет острый угол с осью , касательная к графику убывающей на функции, () образует тупой угол с осью . Если функция на является постоянной , , то и касательная к графику функции параллельна оси .

Точка называется Точкой локального максимума (минимума) функции если существует -окрестность точки , такая, что для всех выполняется неравенство (рисунок 6.1)

().

Значение называется Локальным максимумом (минимумом) функции.

Обозначается:

().

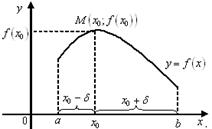
Рисунок 6.1 – Локальный максимум

Точки максимума или минимума функции называются Точками экстремума функции, а максимумы и минимумы функции называются Экстремумами функции.

Экстремумы функции носят локальный характер – это наибольшее или наименьшее значения функции по сравнению с близлежащими ее значениями.

Если функция на имеет несколько максимумов и минимумов, то возможен случай, когда максимум функции меньше ее минимума.

Наименьшее и наибольшее значения функции на называются Абсолютными минимумом и Максимумом или Глобальными экстремумами функции

Обозначаются: , .

< Предыдущая		Следующая >