01.5. Решение типовых примеров

1 Пользуясь определением производной, найти значение производной функции в точке:

А) в точке ,

Б) , в произвольной точке ,

В) , , в произвольной точке .

Решение. а) находим приращение функции в точке :

.

Тогда по определению

Б) имеем:

.

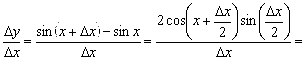
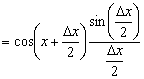Поэтому

.

В) для функции , , получим

.

Тогда

.

2 Доказать, что функция в точке не является дифференцируемой.

Решение. Очевидно, что эта функция определена и непрерывна на множестве . Вычислим производную функции справа в точке .

При имеем , .

Поэтому

.

Аналогично при получим , .

Следовательно, производная слева равна

.

Поскольку , то функция в данной точке производной не имеет.

Следовательно, она не дифференцируема в этой точке.

3 Найти дифференциал функции в точке .

Решение. Используя определение дифференциала, находим:

.

Откуда .

4 Вычислить приближенно с помощью дифференциала значение .

Решение. Рассмотрим функцию .

Так как , и

, , ,

То по формуле (1.1) получаем:

.

5 Составить уравнения касательной и нормали к графику функции в точке .

Решение. Имеем:

, , .

Поэтому искомое уравнение касательной по формуле (1.3) запишется так

,

А уравнение нормали по формуле (1.4) примет вид:

.

6 Вычислить и сравнить на промежутке мгновенные скорости двух точек, прямолинейные движения которых заданы уравнениями , .

Решение. Находим мгновенные скорости точек в момент времени :

,

.

Отсюда получаем: .

Видно, что выполняется неравенство , и – неравенство .

Следовательно, в точке имеем

.

7 Используя правила дифференцирования и таблицу производных, вычислить производные следующих функций:

А) , б) , в) .

Решение. а) перепишем функцию в виде:

.

Применяя правило дифференцирования суммы, получим:

.

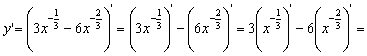
Б) по правилу дифференцирования дроби имеем:

.

В) используя правила дифференцирования суммы и произведения, получим:

.

< Предыдущая		Следующая >