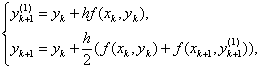4.3.2. Метод Эйлера и его модификации
Будем искать решение задачи (6) в прямоугольнике
![]() .
.
Введем сетку на оси ![]()
![]() ,
, ![]() ,
, ![]() .
.
Простейший итерационный процесс решения задачи (6) получается, если аппроксимировать производную ![]() на сетке
на сетке ![]() правой конечной разностью. Обозначая приближенное решение на сетке
правой конечной разностью. Обозначая приближенное решение на сетке ![]() , получим
, получим
![]()
Или
|
|
(10) (10) |
Итерационная процедура (10) представляет собой Метод Эйлера (или Метод ломаных). Графическая иллюстрация метода приведена на рис. 4.1
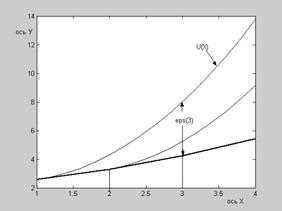
Рис. 4.1. Графическая иллюстрация метода Эйлера (метод ломаных). Жирная кривая – ломаная Эйлера;
U(x) – интегральная кривая, проходящая через начальную точку (1, U(1));
Шаг сетки h = 1. eps(3) – погрешность в точке X2 = 3.
Начав движение из точки ![]() на точном решении
на точном решении ![]() , итерационное решение образует ломаную линию, каждый отрезок которой представляет собой касательную к кривой
, итерационное решение образует ломаную линию, каждый отрезок которой представляет собой касательную к кривой ![]() , проходящую через данную точку.
, проходящую через данную точку.
Действительно, запишем уравнение касательной к U(X) в точке ![]() и положим
и положим ![]() :
:
![]() .
.
Далее, аналогичным образом, строим касательную в точке ![]() и положим
и положим ![]()
![]() и т. д.
и т. д.
Здесь ![]() – та интегральная кривая, которая проходит через точку (X1,Y1).
– та интегральная кривая, которая проходит через точку (X1,Y1).
Из рисунка видно, что ошибка ![]() растет с номером K. Выясним, каков порядок этой ошибки в сеточной норме
растет с номером K. Выясним, каков порядок этой ошибки в сеточной норме
![]() .
.
Будем считать, что ошибка округления имеет порядок не меньший, чем ![]() . Тогда из (10) следует:
. Тогда из (10) следует:
|
|
(11) |
Разложим точное решение ![]() в точке
в точке ![]() с такой же точностью:
с такой же точностью:
|
|
(12) |
Вычтем(12) из (11) Þ
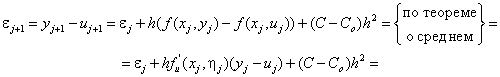
|
|
(13) |
Где ![]() .
.
В силу условий теоремы существования и единственности частные производные ![]() ограничены в прямоугольнике
ограничены в прямоугольнике ![]() :
: ![]() .
.
Обозначим ![]() и оценим (13) по модулю
и оценим (13) по модулю
|
|
![]() по условию.
по условию.
Обозначим
|
|
(10) (14) |
Теорема 4.4. Для метода Эйлера имеет место следующая оценка погрешности:
|
|
(11) (15) |
![]() Из (14) следует (используем рекурсию «назад»):
Из (14) следует (используем рекурсию «назад»):

Используя алгебраическое тождество
![]()
Получаем:
|
|
(12) |
В последнем неравенстве использован второй замечательный предел.
Учитывая, что
![]()
Получаем
![]() ,
,
Т. е. оценку (15). ![]()
Замечание. Из соотношений (14) и (15) следует, что
1. Ошибка растет с номером шага K.
2. Порядок ошибки в методе Эйлера ![]() .
.
Рассмотрим несколько модификаций метода Эйлера повышенной точности.
Метод предиктор-корректор. Проинтегрируем обе части уравнения (6) по отрезку ![]() на равномерной сетке
на равномерной сетке ![]() :
:
![]() .
.
Левую часть полученного уравнения вычисляем по формуле Лейбница:
![]() .
.
Для вычисления правой части используем квадратурную формулу трапеций:
![]()
Где ![]() погрешность, определяемая формулой
погрешность, определяемая формулой
![]() .
.
Если отбросить остаточный член, то получаем Неявную итерационную схему.
|
|
(13) (16) |
Аналогично тому, как оценивается ошибка в методе Эйлера, можно показать, что результирующая ошибка метода (16) имеет порядок ![]() (теряется один порядок при приближении к концу отрезка).
(теряется один порядок при приближении к концу отрезка).
Т. к. схема (16) неявная, то ее следует решать методом итераций для фиксированных точек ![]() и
и ![]() . Более простой путь заключается в следующем. Используем в (16) только 2 последовательных этапа итераций:
. Более простой путь заключается в следующем. Используем в (16) только 2 последовательных этапа итераций:
|
|
(14) (17) |
![]() .
.
Полученная схема (17) имеет также порядок точности ![]() и носит название «Метод предиктор-корректор» (Метод Хойна - в иностранной литературе).
и носит название «Метод предиктор-корректор» (Метод Хойна - в иностранной литературе).
Поясним геометрический смысл названия.
На первом этапе Предсказывается значение ![]() по методу Эйлера. На втором этапе это значение Корректируется путем усреднения угловых коэффицинтов в точках
по методу Эйлера. На втором этапе это значение Корректируется путем усреднения угловых коэффицинтов в точках ![]() и
и ![]() . За счет коррекции точность метода и повышается на порядок
. За счет коррекции точность метода и повышается на порядок ![]() по сравнению с методом Эйлера.
по сравнению с методом Эйлера.
Метод средней точки. Найдем сначала значение ![]() в промежуточной точке
в промежуточной точке ![]() отрезка
отрезка ![]() по простому методу Эйлера.:
по простому методу Эйлера.:
![]() - обозначим так найденное значение
- обозначим так найденное значение ![]() на половинном шаге от точки
на половинном шаге от точки ![]() . Затем в полученной точке
. Затем в полученной точке  вычислим угловой коэффициент касательной
вычислим угловой коэффициент касательной  и в этом направлении совершим движение из точки
и в этом направлении совершим движение из точки ![]() в точку
в точку ![]() :
:
 .
.
Полученный метод имеет 2-ой порядок точности и называется Модифицированным методом Эйлера С коррекцией углового коэффициента на половинном шаге или более коротко─Метод средней точки.
Существует общий теоретический подход к построению явных итерационных методов решения задачи Коши повышенного порядка точности ![]() . Это так называемые Методы Рунге-Кутты
. Это так называемые Методы Рунге-Кутты ![]() -го порядка, удовлетворяющие следующим условиям.
-го порядка, удовлетворяющие следующим условиям.
1. Это одношаговые методы, т. е. при переходе из точки ![]() в точку
в точку ![]() используется лишь информация о предыдущей точке
используется лишь информация о предыдущей точке ![]() .
.
2. Процедура согласуется с рядом Тейлора вплоть до членов порядка ![]() , где
, где ![]() - порядок метода.
- порядок метода.
3. Метод не использует производных от ![]() , а требует только вычисления функции в различных точках сетки, причем число вычислений функции - минимально возможное для данного порядка.
, а требует только вычисления функции в различных точках сетки, причем число вычислений функции - минимально возможное для данного порядка.
Заметим, что метод Эйлера является частным случаем метода Рунге-Кутты, имеющий наименьший первый порядок точности, а методы средней точки и предиктор-клрректор - методы Рунге-Кутты второго порядка.
Остановимся вкратце на средствах пакета MATLAB решения задачи Коши. В среде МАТЛАБ реализованы следующие процедуры Рунге-Кутты:
Ode23 – метод второго и третьего порядка;
Ode45 - метод четвертого и пятого порядка;
Ode113 – многошаговый метод Адамса переменного порядка;
При практическом применении методов повышенной точности возникает вопрос, какой формулой пользоваться на практике? Если априори известно, что ![]() - достаточно гладкая функция, например,
- достаточно гладкая функция, например, ![]() , то наиболее эффективна процедура ode45 или ode113. Если же гладкость функции
, то наиболее эффективна процедура ode45 или ode113. Если же гладкость функции ![]() недостаточна, то лучше использовать методы второго и третьего порядка. В лабораторной работе 7 предусмотрено знакомство с этими командами.
недостаточна, то лучше использовать методы второго и третьего порядка. В лабораторной работе 7 предусмотрено знакомство с этими командами.
| < Предыдущая | Следующая > |
|---|