4.3.1. Задача Коши для ОДУ. Постановка задачи

Задача Коши для ОДУ первого порядка для функции одной переменной ставится следующим образом:

(6)

Более общая постановка задачи Коши для дифференциального уравнения N-го порядка:

(7)

Здесь - заданные числа (начальные условия).

Задача (7) с помощью замены переменных

,

Сводится к системе дифференциальных уравнений первого порядка:

(8)

Систему (8) можно переписать в векторном виде:

,

(9)

Где , ,

.

Система (9) исследуется и решается аналогично одномерной задаче Коши (6), поэтому важно изучить, прежде всего, численные методы решения задачи (6).

В курсе математического анализа формулируется и доказывается теорема существования и единственности решения задачи Коши. Отметим, что для выполнения теоремы необходимо и достаточно, чтобы функция имела непрерывные частные производные по в замкнутой ограниченной области на плоскости .

< Предыдущая		Следующая >
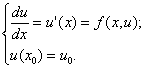
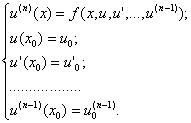
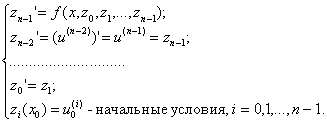
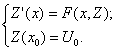