4.2. Численное дифференцирование на равномерной сетке
Пусть задана сетка ![]() .
.
Теорема 4.1. Обозначим ![]() и т. д. и пусть
и т. д. и пусть ![]() , тогда существует такая точка
, тогда существует такая точка ![]() , для которой справедлива формула:
, для которой справедлива формула:
|
|
(2) |
![]() Т. к.
Т. к. ![]() , то справедливо разложение Тейлора с центром в точке
, то справедливо разложение Тейлора с центром в точке ![]() и остаточным членом в форме Лагранжа:
и остаточным членом в форме Лагранжа:
![]() .
.
В точке ![]() получаем:
получаем:
![]() ,
,
Откуда следует
![]() ,
,
Что и требовалось доказать. ![]()
Теорема 4.2. Пусть ![]() тогда
тогда
|
|
(3) |
![]() Самостоятельно. См. ход доказательства следующей теоремы
Самостоятельно. См. ход доказательства следующей теоремы ![]() .
.
Теорема 4.3. Пусть ![]() , тогда существует такая точка
, тогда существует такая точка ![]() , что справедлива формула
, что справедлива формула
|
|
(4) |
![]() По условию теоремы справедливо тейлоровское разложение функции
По условию теоремы справедливо тейлоровское разложение функции ![]() с центром в точке
с центром в точке ![]() :
:
![]() , (5)
, (5)
Где ![]() . Положим в формуле (5) последовательно
. Положим в формуле (5) последовательно ![]() и
и ![]() :
:
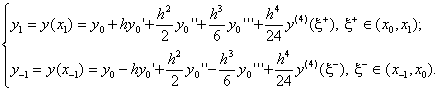
Складывая эти две формулы, получим
![]() .
.
В силу непрерывности четвертой производной ![]() :
:
![]() ,
,
Откуда следует:
![]() , т. е. формула (4)
, т. е. формула (4) ![]() .
.
Замечание. Формулы (2), (3) и (4) называются Формулами численного дифференцирования. При этом формула (2) Аппроксимирует первую производную в узле ![]() Правой конечной разностью и имеет Порядок точности
Правой конечной разностью и имеет Порядок точности ![]() (т. е. Первый порядок);
(т. е. Первый порядок);
Формула (3) аппроксимирует первую производную центральной конечной разностью и имеет Порядок точности ![]() (Второй порядок);
(Второй порядок);
Формула (4) аппроксимирует вторую производную в узле ![]() центральной конечной разностью и имеет Порядок точности
центральной конечной разностью и имеет Порядок точности ![]() .
.
| < Предыдущая | Следующая > |
|---|