4.1. Численные методы решения обыкновенных дифференциальных уравнений (ОДУ). Численное дифференцирование на основе интерполяции
Если функция ![]() задана таблично, то аналитическое дифференцирование невозможно. Строится интерполяционный полином и его производную принимают приближенно за
задана таблично, то аналитическое дифференцирование невозможно. Строится интерполяционный полином и его производную принимают приближенно за ![]() .
.
Запишем 1-ую форму интерполяционного полинома Ньютона на равномерной сетке:
|
|
(1) |
Где ![]()
![]() .
.
![]() - погрешность интерполяции.
- погрешность интерполяции.
Дифференцируя (1), получим:
![]() ,
,
Где
![]() -
-
- теоретическая погрешность производной.
Пример 1. Пусть ![]() . Вычислить приближенно первую производную
. Вычислить приближенно первую производную ![]() и оценить погрешность (теоретическую).
и оценить погрешность (теоретическую).
![]() На данной сетке получаем:
На данной сетке получаем: ![]() .
.
Интерполяционный полином третьего порядка имеет вид:
![]() ;
;
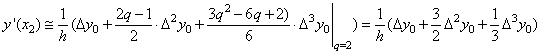 ;
;
![]() .
. ![]()
| < Предыдущая | Следующая > |
|---|