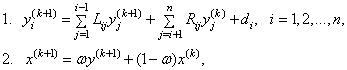3.5.5. Стационарные итерационные процедуры
Пусть задана система ЛАУ (23) общего вида (первого рода)
|
|
(1) |
Требуется привести данную систему к виду
|
X=Tx+D |
(2) |
С матрицей (оператором) Т, Удовлетворяющей условию ![]() в какой либо матричной норме.
в какой либо матричной норме.
Рассмотрим простейший прием такого преобразования – тождественное преобразование:
|
|
( (31) |
Где Н - некоторая невырожденная матрица.
Из (31) следует, что
|
X=Tx+d, Где |
( (32) |
Определение 1. Итерационная процедура, основанная на представлениях (31)-(32)
|
|
(5) |
Называется Линейной стационарной итерационной процедурой; при этом матрица Т в представлении (32) называется Матрицей перехода, а матрица Н – матрицей расщепления.
Определение 2. Более общая Линейная нестационарная итерационная процедура записывается в виде:
![]() ,
,
Где Hk – матрица расщепления k-го шага. Соответственно матрица перехода Tk=E-HkA – Называется Матрицей перехода k-го шага.
Рассмотрим некоторые частные случаи стационарных процедур, зависящих от выбора матрицы ![]() .
.
I. Метод простых итераций ( Метод Ричардсона).
Положим ![]() . Матрица перехода в этом случае имеет вид:
. Матрица перехода в этом случае имеет вид:
![]() .
.
Получаем так называемый метод Простых итераций или Метод Ричардсона.
![]() , или
, или ![]() .
.
Выясним условия сходимости метода Ричардсона.
Пусть ![]() - собственное значение матрицы
- собственное значение матрицы ![]() ,
, ![]() - собственное значение матрицы
- собственное значение матрицы ![]() .
. ![]() является корнем характеристического уравнения
является корнем характеристического уравнения
![]() .
.
![]() - корнем уравнения
- корнем уравнения
![]() ,
,
Или: ![]() , откуда следует, что
, откуда следует, что
![]() .
.
Согласно теореме 3.8. условие сходимости:
![]() .
.
Последнее условие, например, выполняется, если ![]() .
.
2. Ускоренный метод Ричардсона.
Пусть ![]() , где
, где ![]() - некоторый параметр сходимости, с помощью которого можно оптимизировать процедуру Ричардсона.
- некоторый параметр сходимости, с помощью которого можно оптимизировать процедуру Ричардсона.
Матрица перехода в этом случае имеет вид:
![]() .
.
Требуется так выбрать параметр ![]() , чтобы минимизировать спектральный радиус
, чтобы минимизировать спектральный радиус ![]() .
.
Теорема 3.9. Пусть ![]()
Тогда ![]() и достигается при
и достигается при ![]() ,
,
Где ![]() - оптимальное значение параметра сходимости ускоренной итерационной процедуры Ричардсона:
- оптимальное значение параметра сходимости ускоренной итерационной процедуры Ричардсона:
![]() .
.
![]() Т. к.
Т. к. ![]() , то все собственные значения матрицы
, то все собственные значения матрицы ![]()
![]() .
.
Выберем в качестве матричной нормы – спектральную норму ![]() . По определению,
. По определению,
![]() ,
,
Поэтому чем меньше радиус сходимости, тем быстрее сходится итерационная процедура в соответствии с принципом сжатых отображений.
Пусть ![]() - собственное значение матрицы
- собственное значение матрицы ![]()
![]() - корень уравнения
- корень уравнения
![]() .
.
Пусть ![]() - собственное значение матрицы
- собственное значение матрицы ![]()
![]()
![]() является корнем уравнения
является корнем уравнения
![]() .
.
Из сравнения двух характеристических уравнений следует:
![]() .
.
Таким образом,
![]() .
.
|
|
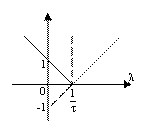
Обозначим ![]() - функция от
- функция от ![]() при фиксированном
при фиксированном ![]() .
.
Т. к. функция ![]() кусочно линейна, то
кусочно линейна, то ![]() достигается на концах отрезка, следовательно
достигается на концах отрезка, следовательно
![]() .
.
Найдем такое ![]() , для которого
, для которого
|
|
(33) |
Не трудно проверить, что при ![]() выполняется следующее условие:
выполняется следующее условие:
![]() ,
,
Т. е. указанное в теореме значение ![]() как раз и является оптимальным в смысле критерия (33). Действительно, пусть, например,
как раз и является оптимальным в смысле критерия (33). Действительно, пусть, например,
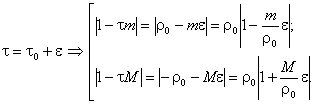
Из последних равенств видно, что при любом знаке ![]() один из модулей будет
один из модулей будет ![]() , т. е.
, т. е. ![]() , что и требовалось доказать.
, что и требовалось доказать. ![]()
Лемма 3.2. Пусть матрица ![]() удовлетворяет условию
удовлетворяет условию ![]() и является вещественной и симметрической, тогда максимальный коэффициент сжатия в ускоренном методе Ричардсона
и является вещественной и симметрической, тогда максимальный коэффициент сжатия в ускоренном методе Ричардсона ![]() может быть записан в виде
может быть записан в виде
![]() ,
,
Где ![]() , и
, и ![]() .
.
![]() Т. к.
Т. к. ![]() , то
, то ![]() , поэтому по свойству 6)
, поэтому по свойству 6)
![]() ,
,
А по свойству 7) собственные числа матриц ![]() и
и ![]() взаимообратны.
взаимообратны.
Отсюда следует, что
![]() ,
, 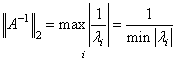 ,
,
И в обозначениях теоремы 3.9. можем записать:
![]() .
.
Т. о.  .
. ![]()
Следствие. Если система первого рода плохо обусловлена (![]() ), то
), то ![]() и метод Ричардсона сходится плохо и становится чувствительным к возмущениям правой части. В этом случае необходимо перейти к более эффективным методам решения СЛАУ (например, к методу сопряженных градиентов, метод минимизации невязки и др. [1,5]).
и метод Ричардсона сходится плохо и становится чувствительным к возмущениям правой части. В этом случае необходимо перейти к более эффективным методам решения СЛАУ (например, к методу сопряженных градиентов, метод минимизации невязки и др. [1,5]).
3. Метод Якоби.
В этом методе приведение системы (23) к виду (27) осуществляется с помощью представления матрицы А в виде:
|
|
(34) |
Где
 -
-
- диагональная матрица,
 -
-
- строго нижняя (lower) треугольная матрица,
 -
-
- строго верхняя (upper) треугольная матрица.
Подставляя представление (34) в систему (23) Ax=b, получаем:
Dx=(CL+CU)X+B,
Откуда следует
![]() ,
,
Где матрица перехода имеет вид:
![]() ,
,
![]() ,
, ![]() – матрица расщепления.
– матрица расщепления.
Получаемый при этом итерационный метод называется Методом Якоби. Необходимое условие сходимости: ![]() (иначе не существует
(иначе не существует ![]() ).
).
Достаточные условия сходимости устанавливаются в следующей теореме:
Теорема 3.10. (О сходимости метода Якоби). Пусть матрица ![]() - вещественная и удовлетворяет условиям:
- вещественная и удовлетворяет условиям:
|
| |
|
|
(35) |
(Условия (35) называются Условиями строгого диагонального преобладания). Тогда метод Якоби сходится.
![]() Условие (35) можно записать в виде:
Условие (35) можно записать в виде:
![]() ,
,
Что эквивалентно условию
 . (36)
. (36)
Поскольку
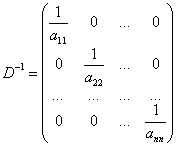 ,
,
То матрица перехода ![]() приобретает вид:
приобретает вид:
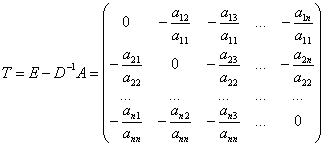 .
.
Воспользуемся строчной нормой матрицы ![]() . Согласно (36):
. Согласно (36):
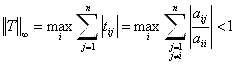 ,
,
И, таким образом, выполняется условие сжатости для данной нормы. Следовательно, метод Якоби сходится в строчной норме. Но поскольку. в ![]() все согласованные матричные нормы эквивалентны, то метод Якоби сходится.
все согласованные матричные нормы эквивалентны, то метод Якоби сходится. ![]()
Замечание. Достаточным условием сходимости метода Якоби является также спектральное условие: ![]() .
.
4. Метод Зейделя (Гаусса-Зейделя).
Метод Якоби может быть оптимизирован следующим образом. Как и в методе Якоби воспользуемся разложением матрицы ![]()
|
|
И запишем систему ![]() в виде:
в виде:
|
|
(11) (37) |
Обозначим
![]()
И подставим в (37):
|
|
(12) (38) |
Нетрудно убедиться, что при покомпонентной записи уравнения (38):
![]()
Вектор ![]() содержит только первые (I-1) компоненты вектора Х, а вектор
содержит только первые (I-1) компоненты вектора Х, а вектор ![]() - Содержит компоненты, начиная с (Xi+1), т. е.
- Содержит компоненты, начиная с (Xi+1), т. е.
|
|
(13) (39) |
При реализации метода последовательных приближений для решения системы (39) естественно использовать в правой части уже найденные значения компонент ![]() , полученные в текущей итерации. Алгоритм Гаусса-Зейделя строится следующим образом:
, полученные в текущей итерации. Алгоритм Гаусса-Зейделя строится следующим образом:
|
|
(14) (40) |
Условия сходимости метода Гаусса-Зейделя (40) те же, что и у метода Якоби, но процедура сходится несколько быстрее.
5. Метод последовательной верхней релаксации.
Дальнейшее ускорение сходимости метода Зейделя может быть достигнуто с помощью введения ускоряющего множителя подобно тому, как это сделано в методе Ричардсона. Получающийся при этом алгоритм носит название Метод последовательной верхней релаксации и реализуется в два этапа:
|
|
(15) (41) |
Где ![]() - ускоряющий множитель (Параметр релаксации).
- ускоряющий множитель (Параметр релаксации).
Доказано (см, например, [1]), что, если матрица ![]() симметрическая и положительно определенная, и
симметрическая и положительно определенная, и ![]() , то итерационная процедура (41) сходится, причем существует такое оптимальное значение параметра
, то итерационная процедура (41) сходится, причем существует такое оптимальное значение параметра ![]() , при котором достигается максимальное ускорение.
, при котором достигается максимальное ускорение.
| < Предыдущая | Следующая > |
|---|
 .
.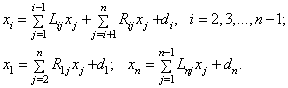
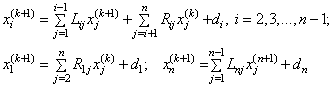 .
.