3.5.4. Итерационные методы решения систем ЛАУ

Рассмотрим вначале систему ЛАУ специального вида

X=Tx+D, , , T - матрица .

(27)

Назовем эту систему системой Второго рода, в отличие от вида системы (23) из параграфа 3.4.3. – системы Первого рода.

Систему второго рода (27) естественно пытаться решать итерационным методом

(28)

В этом методе используются лишь операции сложения и умножения, и не используется операция обращения матрицы – наиболее опасная для накопления ошибок.

Теорема 3.6. Для любой согласованной матричной нормы имеет место неравенство .

Пусть - собственный вектор матрицы , - соответствующее собственное значение. Тогда справедлива следующая цепочка равенств и неравенств:

, в силу согласованности норм. Отсюда получаем

. В силу произвольности собственного значения , получаем требуемый результат .

Теорема 3.7. (Достаточное условие сходимости). Пусть система (1) невырождена, т. е. имеет единственное решение , матрица - вещественная, причем (в какой-либо матричной форме), тогда итерационная процедура (28) сходится к решению при со скоростью геометрической прогрессии.

.Поскольку - решение системы (27), то . Найдем разность

.

Обозначим - вектор ошибки K-Ого шага. Тогда получаем итерационную процедуру

(29)

Оператор - линейный и отображает в себя. Согласно основному принципу сжатых отображений (теорема 3.1, замечание 2) для банахова пространства): если оператор T удовлетворяет условию Липшица с константой

То оператор T в уравнении (29) – сжимающий и выполняется принцип сжатых отображений.

В нашем случае имеем:

.

Т. к. по условию оператор - сжимающий и, следовательно, существует единственная неподвижная точка уравнения

(30)

Обозначим эту точку . Таким образом выполняютя уравнения:

и, кроме того, по определентю . Отсюда

,

Откуда получаем: . Из единственности решения системы (27) получаем:

, т. е. и итерационная процедура (28) сходится к единственной неподвижной точке со скоростью геометрической прогрессии .

Теорема 3.8. (Спектральный признак сходимости). Для сходимости метода простых итераций СЛАУ второго рода необходимо и достаточно, чтобы .

Необходимость. Заметим, что если оператор удовлетворяет условию сжатости, то согласно теореме 3.6 .

Пусть теперь известно, что итерационная процедура (28) сходится при . От противного: пусть и - соответствующий собственный вектор. Выберем начальное приближение и запустим итерационную процедуру (29).

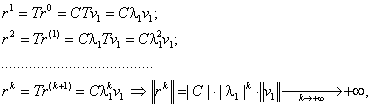
Что противоречит сходимости при начальном приближении .

Достаточность. Докажем для частного случая, когда - вещественная и симметрическая матрица.

Выберем спектральную норму (норму -2):

, где - сингулярные числа матрицы .

Согласно свойству 6) , где - собственные значения матрицы . - т. е. получили достаточное условие сходимости согласно теореме 3.7. в норме -2.

Т. к. все матричные нормы эквивалентны, то сходимость в норме -2 влечет за собой сходимость и в остальных нормах.

< Предыдущая		Следующая >