3.5.3. Обусловленность матриц и систем уравнений
Пусть дана система ЛАУ с невырожденной матрицей А ![]() :
:
|
Ax=B, |
(23) |
И пусть вектор правой части B вычисляется с ошибкой ![]() .
.
Заменим правую часть “возмущенным” значением ![]() , тогда решение приобретет ошибку
, тогда решение приобретет ошибку ![]() и система примет вид:
и система примет вид:
|
|
(24) |
Оценим относительную ошибку решения ![]() в зависимости от относительной величины возмущения правой части
в зависимости от относительной величины возмущения правой части ![]() .
.
Из (23) и (24) следует: ![]() или
или ![]() .
.
Из совокупности равенств
|
|
(25) |
С другой стороны, из (23) следует
![]() .
.
Последнее неравенство подставим в (25)
|
|
(26) |
Определение 6. Число ![]() называется Числом обусловленности матрицы А.
называется Числом обусловленности матрицы А.
Таким образом, из (26) следует, что относительная ошибка решения пропорциональна числу обусловленности матрицы А:
![]() .
.
Если ![]() (система уравнений Плохо обусловлена), то небольшие погрешности вычисления правой части (небольшие “возмущения”) могут приводить к весьма большим отклонениям от точного решения.
(система уравнений Плохо обусловлена), то небольшие погрешности вычисления правой части (небольшие “возмущения”) могут приводить к весьма большим отклонениям от точного решения.
Заметим, что это явление не связано с явлением неустойчивости (т. е. накоплением ошибок при вычислениях), а является следствием специфического свойства матрицы А и наблюдается даже в том случае, когда все вычисления делаются абсолютно точно, а возмущение правой части вызвано неточностями начальных данных при формировании системы.
Примеры плохо обусловленных систем рекомендуется рассмотреть на семинаре и лабораторной работе.
| < Предыдущая | Следующая > |
|---|
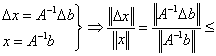 {согласованность матриц}
{согласованность матриц}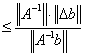 .
.