3.5.2. Нормы векторов и матриц

Пусть - вектор-столбец, . Приведем некоторые известные нормы векторов:

1. - эклидова норма вектора;

2. 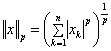- так называемая -Норма, или Норма Гильберта-Шмидта (при совпадает с эвклидовой нормой, а при совпадает с так называемой 1-нормой).

3. - Чебышевская норма.

Все эти нормы в эквивалентны: сходимость в одной из этих норм влечет за собой сходимость в другой (следствие конечности ).

Перейдем к понятию Матричной нормы. Пусть - множество квадратных вещественных матриц порядка . Пусть каждой матрице поставлено в соответствие число . Это число называется Нормой матрицы A, если выполняются следующие аксиомы:

1. ;

2. ;

3. - неравенство треугольника;

4. - кольцевое свойство.

Определение 1. Норма называется Мультипликативной, если выполняются все четыре аксиомы, и Аддитивной, если выполняются только первые три аксиомы.

Определение 2. Если матричная норма удовлетворяет условию

, где ,

(1)

То такая норма называется Согласованной с нормой вектора.

Большинство используемых в числовом анализе матричных норм согласованы с той или иной векторной нормой.

Определим некоторые наиболее употребительные на практике матричные нормы.

-

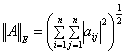- Евклидова норма или норма Фробениуса (Norm(A,‘Fro’) - в MATLAB).

-

- Спектральная норма (Norm(A)=Norm(A,2) в MATLAB),

Где - собственные значения симметричной матрицы (сингулярные числа матрицы А). Обе указанные нормы согласованы с эвклидовой нормой вектора .

-

- Столбцовая норма (Norm(A,1)). (Согласована с векторной нормой ).

-

- строчная норма (Norm(A,Inf)). (Согласована с ).

Замечание. Из всех приведенных матричных норм, согласованных с евклидовой нормой вектора, спектральная норма принимает минимальное значение.

Определение 3. Число (вообще говоря, комплексное) называется Собственным значением матрицы А, соответствующим собственному вектору X, если выполняется условие:

.

(20)

Определение 4. Множество всех собственных чисел матрицы А , записанных с учетом их кратности, называется Спектром матрицы А и обозначается S(A).

Определение 5. Спектральным радиусом r(A) квадратной матрицы А называется максимальное по модулю собственное значение матрицы A.

Система (20) эквивалентна следующей однородной системе уравнений:

.

(21)

Как известно из курса линейной алгебры, система (21) имеет нетривиальные решения тогда и только тогда, когда

.

(22)

Уравнение (22) - алгебраическое уравнение N-ой степени относительно . Все его корни – собственные значения матрицы А.

Определение 6. Сингулярным числом матрицы А называется собственное значение матрицы .

Определение 7. Матрица А называется положительно (неотрицательно) определенной (пишут: или ), если соответствующая квадратичная форма

.

Простейшие следствия из определений.

Следствие 1. (Критерий Сильвестра). все ведущие угловые миноры матрицы А положительны. доказывается в курсе линейной алгебры

Следствие 2. , причем .

следует из критерия Сильвестра.

Следствие 3. все собственные значения . (Для ).

Пусть - собственное значение, соответствующее собственному вектору V. По условию

.

Следствие 4. Пусть А – вещественная матрица матрица .

Имеем: {по свойству скалярного произведения}.

Следствие 5. Сингулярные числа вещественной матрицы А – неотрицательны.

Следует из С.3 и С.4.

Следствие 6. Пусть А – вещественная и симметрическая матрица .

Имеем: .

Следствие 7. Если А – невырожденная матрица собственные значения матриц А и A-1 взаимообратны.

Пусть результат.

< Предыдущая		Следующая >