4.4.1. Численные методы решения краевых задач для ОДУ. Постановка задачи для диффернциального уравнения 2-го порядка

Рассмотрим вначале общую нелинейную постановку краевой задачи для ОДУ второго порядка:

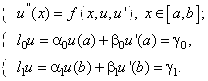(18)

В постановке задачи (18) принята следующая классификация граничных условий:

При - краевые условия – Однородные; при - краевое Условие первого рода на левом конце; при - краевое условие Второго рода на левом конце; при - краевые условия Третьего рода на левом конце. На правом конце отрезка краевые условия классифицируются аналогично.

Отметим основное отличие краевой задачи (18) от задачи Коши: в задаче Коши начальные условия задаются в одной точке (как правило, на левом конце отрезка), а в краевой задаче – на обоих концах. Естественно попытаться свести краевую задачу к задаче Коши, т. к. для нее разработаны эффективные приближенные методы решения. Таковым, например, является Метод стрельбы.

Для простоты рассмотрим задачу (18) с краевыми условиями первого рода:

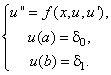(19)

Заменим задачу (19) на следующую задачу Коши:

(20)

Решаем задачу (20) подходящим методом Рунге-Кутты. Обозначим полученное решение и вычислим величину - погрешность решения на правом конце. Корректируем угловой коэффициент на левом конце в зависимости от знака погрешности, заменяя его на . Находим новое решение и т. д. до тех пор, пока не выполнится условие , где - заданная погрешность. Название метода связано с его геометрической интерпретацией: Стрельба из точки с координатами под углом, определяемым угловым коэффициентом .

< Предыдущая		Следующая >