2.4. Некоторые общие свойства ортогональных с весом полиномов

Пусть - система ортогональных с весом на отрезке полиномов. Справедливы следующие общие свойства таких полиномов.

1. Многочлен ортогонален любому алгебраическому многочлену M-ой степени при .

Действительно, многочлен можно единственным образом представить в виде линейной комбинации

.

(17)

Равенство (17) тождественное, поэтому коэффициенты единственным образом вычисляются путем приравнивания коэффициентов при соответствующих степенях X.

Умножая обе части (17) скалярно на , имеем:

в силу ортогональности .

2. Полином имеет на отрезке ровно N действительных и различных корней.

Заметим, что в силу теоремы Гаусса многочлен не может иметь более, чем N корней (вообще говоря, комплексных).

Пусть имеет меньше, чем N простых действительных корней. Обозначим их . По этим точкам построим фундаментальный многочлен

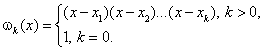
Рассмотрим многочлен - многочлен степени , который имеет нули четной кратности. Следовательно, он сохраняет знак на . Отсюда следует, что

, т. е. , что противоречит свойству 1.

3. Для всех ортогональных многочленов, построенных на канонических промежутках с соответствующими весовыми функциями, существуют формулы Родрига и рекуррентные формулы. В частности, соответствующие формулы для полиномов Лагранжа приведены в лекции 5.

4. Система ортогональных с весом полиномов на - полна. Это значит, что не существует функции, отличной от нулевой и ортогональной всем функциям системы, т. е. из равенств следует, что на .

< Предыдущая		Следующая >