2.5.Квадратурные формулы Гаусса-Кристоффеля

Рассмотрим общую задачу численного интегрирования с весовой функцией .

При построении квадратурных формул интерполяционного типа на бесконечных интервалах необходимо ввести дополнительно условие на весовую функцию:

.

(1)

Запишем квадратурную формулу для произвольного, но фиксированного распределения узлов

: .

(18)

При построении квадратурных формул Ньютона-Котеса узлы распределялись равномерно по отрезку . Очевидно, что такой способ выбора узлов становится невозможным для несобственных интегралов с бесконечными пределами. Возникает вопрос: как выбрать систему узлов квадратурной формулы, чтобы формула (16) имела наивысшую возможную алгебраическую степень точности? Напомним, что квадратурная формула имеет алгебраическую степень точности , если она точна для многочленов степени меньшей или равной . Заметим, что формула (16) содержит всего 2N неизвестных параметров (N узлов и N весовых коэффициентов). Столько же коэффициентов содержит и произвольный многочлен степени . Таким образом, наивысшая алгебраическая степень точности формулы (2*) не может быть больше .

Определение 1. Квадратурная формула (16), обеспечивающая условие:

Называется Квадратурной формулой наивысшей алгебраической степени точности.

Теорема 2.3. Для того чтобы формула (18) была квадратурной формулой наивысшей алгебраической степени точности, необходимо и достаточно, чтобы узлы совпадали с нулями полинома из системы ортогональных полиномов с весом на .

Необходимость. Пусть формула (18) имеет наивысшую алгебраическую степень точности. По определению это значит, что , где - семейство многочленов степени .

Как и при выводе интерполяционных формул, обозначим

-

- полином N-Ой степени, нули которого совпадают с узлами интерполяции.

Рассмотрим функцию .

Т. к. - алгебраический многочлен степени , то по условию теоремы . Но т. к. , то из (18) следует, что

.

(19)

Из равенства (19) усматриваем, что , т. е многочлен ортогонален системе для .

Рассмотрим вспомогательную функцию , где - коэффициент при старшей степени многочлена . Очевидно, что - многочлен степени . Рассмотрим скалярное произведение

.

Пусть , тогда

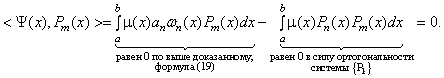
Пусть теперь тогда в силу свойства 1) ортогональных полиномов (степень полинома меньше чем ).

Т. о. ортогональна всем полиномам системы . Отсюда, в силу свойства 4) ортогональных полиномов, следует, что .

Последнее равенство означает, что - нули полинома .

Достаточность. Пусть - нули полинома , и - полином степени . Требуется доказать, что для .

Очевидно, достаточно рассмотреть случай (если формула точна для многочлена степени , то она автоматически точна и для многочлена любой меньшей степени).

Пусть . Представим этот многочлен в виде:

,

(20)

Где

- многочлен -ой степени (частное от деления на ),

, - многочлен степени (остаток от деления).

Т. к. - корни полинома , то из (4) следует, что

, т. е. является интерполяционным многочленом для , следовательно

,

(21)

Где - фундаментальный многочлен Лагранжа -ой степени.

Учитывая (20) и (21), распишем интеграл:

=

.

(22)

Формула (22) - квадратурная формула интерполяционного типа с погрешностью

для , а, значит, и для любого многочлена степени .

Заметим, что единственность квадратурной формулы (16) следует из единственности нулей ортогонального полинома Pn(X).

Определение 2. Квадратурная формула (18) наивысшей алгебраической степени точности носит название Формулы Гаусса-Кристоффеля, а весовые коэффициенты - Коэффициентов Кристоффеля.

Теорема 2.4. (О свойствах коэффициентов Гаусса-Кристоффеля). Пусть

-

(23)

Формула Гаусса-Кристоффеля. Тогда весовые коэффициенты Кристоффеля удовлетворяют следующим условиям:

1) ;

2) ;

3) ,

Где - фундаментальные полиномы Лагранжа, построенные по узлам , являющимися нулями полинома из соответствующей ортогональной системы.

По доказанному в теореме 2.3, формула (23) точна для многочленов порядка , в частности, для . Отсюда следует, что

, т. е. свойство 2).

Возьмем далее в качестве полином степени , например:

- фиксированные.

Учитывая свойство фундаментальных многочленов Лагранжа :

,

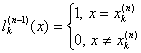и, подставляя данный многочлен в (23), получим:

.

Вследствие свойства 1) фундаментального полинома Лагранжа из последнего равенства следует, в частности, что . Таким образом, все свойства доказаны.

Замечание 1. Для остаточного члена квадратурной формулы Гаусса-Кристоффеля (23) справедливо представление:

,

Где , - нули полинома , xÎ(a, b).

Без доказательства.

Замечание 2. Классические ортогональные многочлены обычно строятся для канонических промежутков: с соответствующими весами .

Таблица 2.1. Основные канонические системы ортогональных многочленов:

П Промежуток	В Весовая функция	Название ортогональной системы	Остаточный член
		Полиномы Лежандра
		Полиномы Чебышева
		Полиномы Лагерра	Смотри в справочной литературе.
		Полиномы Эрмита

Самая простая формула Гаусса-Кристоффеля имеет место для промежутка с весом (используются нули полинома Чебышева ):

,

Где

.

Замечание 3. Для произвольного конечного промежутка и , с помощью линейного преобразования

Интеграл приводится к каноническому промежутку.

Пример 2. Вычисляется интеграл

С помощью квадратурной формулы Гаусса-Кристоффеля порядка . Оценить по модулю остаточный член .

Согласно случаю 2) из таблицы:

,

Где .

Пример 3. Вычисляется интеграл

С помощью квадратурной формулы Гаусса-Кристоффеля порядка . Оценить по модулю и указать саму формулу.

- нули многочлена Лежандра (см. пример 16 п. п. 1.8 и семинарское занятие С-3):

, .

Найдем нули полинома :

, , .

Для вычисления коэффициентов Кристоффеля используем формулу для полиномов Лежандра из таблицы 2.1. Для этого найдем сначала значения :

. Подставляя найденные значения в формулу для коэффициентов , получаем: . Отсюда следует формула Гаусса-Кристоффеля 3-го порядка, приближающая указанный интеграл:

.

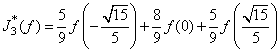Погрешность данного приближения вычисляем по формуле для из первой строки таб.2.1:

.

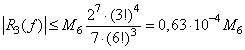< Предыдущая		Следующая >