2.3. Квадратурные формулы Ньютона-Котеса
При построении базовых квадратурных формул использовалось число узлов от одного до трех, распределенных равномерно на отрезке ![]() .
.
Для повышения точности квадратурных формул введем на ![]() более густую равномерную сетку с мелким шагом H:
более густую равномерную сетку с мелким шагом H:
![]()
И вычислим подынтегральную функцию в полученных узлах
![]() .
.
Используя полученное разбиение отрезка, запишем интеграл
![]() .
.
Дальнейший результат будет зависеть от порядка базовой квадратурной формулы, используемой на I-ом интервале. Например, для приближения порядка ![]() (формула трапеций) получим:
(формула трапеций) получим:
|
|
(13) |
Формулу (13) можно назвать «Обобщенной формулой трапеций».
Определение. Квадратурная формула N-го порядка, построенная на равномерной сетке с (N+1) узлом, носит название «Формула Ньютона-Котеса порядка n с (N+1) Узлом».
Т. о. формула (13) есть формула Ньютона-Котеса порядка N=1 c (N+1) узлом. Выведем формулу для погрешности данной квадратурной формулы.
Теорема 2.1. Пусть ![]() и
и ![]() - равномерная сетка узлов с шагом
- равномерная сетка узлов с шагом ![]() , и
, и ![]() , где
, где ![]() определяется формулой (11). Тогда для погрешности обобщенной формулы трапеций справедлива формула:
определяется формулой (11). Тогда для погрешности обобщенной формулы трапеций справедлива формула:
![]() (14)
(14)
![]() Обозначим погрешность базовой формулы трапеций на J-М интервале
Обозначим погрешность базовой формулы трапеций на J-М интервале
![]() , где
, где ![]() ,
, ![]() .
.
Просуммируем все J-ые погрешности по N интервалам:
![]() .
.
Т. к. по условию ![]() , то
, то ![]() непрерывна на
непрерывна на ![]() . Отсюда следует, что функция
. Отсюда следует, что функция ![]() так же непрерывна на
так же непрерывна на ![]() , причем из условия
, причем из условия ![]() следует, что
следует, что ![]() .
.
Далее по теореме о промежуточном значении непрерывной на отрезке ![]() функции получаем, что найдется такая точка
функции получаем, что найдется такая точка ![]() , что
, что ![]() .
.
Отсюда для погрешности формулы Ньютона-Котеса порядка 1 получаем:
|
|
(2) |
В таком виде формула (14) демонстрирует степень зависимости погрешности от числа интервалов N. ![]()
Пусть ![]() . Построим формулу Ньютона-Котеса второго порядка, обобщающую квадратурную формулу Симпсона. Для этого необходимо на
. Построим формулу Ньютона-Котеса второго порядка, обобщающую квадратурную формулу Симпсона. Для этого необходимо на ![]() распределить нечетное число узлов:
распределить нечетное число узлов:
![]() . Диаграмма узлов изображена
. Диаграмма узлов изображена
На рисунке: 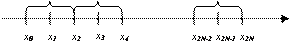
![]()
На каждой последовательной тройке узлов ![]() используем базовую формулу Симпсона.
используем базовую формулу Симпсона.
Обозначим ![]()
Имеем:
![]()
![]()
|
|
(15) |
Оценим погрешность обобщенной формулы Симпсона (15).
Теорема 2.2. Пусть ![]() и
и ![]() -равномерная сетка узлов с шагом
-равномерная сетка узлов с шагом ![]() на
на ![]() . Тогда для погрешности обобщенной формулы Симпсона справедлива формула:
. Тогда для погрешности обобщенной формулы Симпсона справедлива формула:
![]() . (16)
. (16)
![]() Теорема доказывается аналогично теореме 2.1, путем суммирования погрешностей на базовых отрезках
Теорема доказывается аналогично теореме 2.1, путем суммирования погрешностей на базовых отрезках
![]()
И использования теоремы Коши о промежуточном значении непрерывной функции на отрезке. ![]()
| < Предыдущая | Следующая > |
|---|