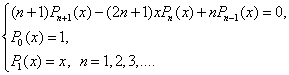1.8.2. Среднеквадратичное приближение функций алгебраическими многочленами
Рассмотрим систему алгебраических многочленов
|
|
(34) |
Такая система, рассматриваемая в гильбертовом пространстве ![]() , линейно независима при
, линейно независима при ![]() .
.
Однако непосредственная подстановка алгебраических многочленов в систему (30) не эффективна, т. к. приводит к плохо обусловленной системе уравнений. На базе системы (34) можно построить ортогональные полиномы на заданном отрезке (или бесконечном промежутке) с заданной весовой функцией ![]() .
.
Рассмотрим один из алгоритмов ортогонализации, известный как Рекуррентная процедура Грама-Шмидта.
Новая система полиномов, ортогональная на ![]() с весом
с весом ![]() строится рекуррентно:
строится рекуррентно:
 .
.
Накладывая условие ортогональности:
![]() ,
,
![]()
получаем формулу для коэффициентов ![]() :
:
|
|
(35) |
Пример 16. Пусть отрезок ![]() . Построить первые три ортогональных полинома
. Построить первые три ортогональных полинома ![]() , используя процедуру Грама-Шмидта.
, используя процедуру Грама-Шмидта.
![]() Полагаем
Полагаем ![]() . Далее по формулам (35) находим
. Далее по формулам (35) находим

Откуда получаем ![]()
Действуя аналогично далее, получаем: ![]() .
. ![]()
Существует другой - более эффективный способ построения ортогональных многочленов. В частности, для системы ортогональных многочленов на отрезке ![]() с весом
с весом ![]() , справедливы следующие две формулы:
, справедливы следующие две формулы:
Формула Родрига:
|
|
(36) |
И
Рекуррентная формула:
|
|
(37) |
Из (36) последовательно получаем: ![]() ; Далее по рекуррентной формуле (37) при
; Далее по рекуррентной формуле (37) при ![]() находим:
находим: ![]() .
.
Получаемые таким образом полиномы называются Полиномами Лежандра.
Замечание. Найденные по процедуре (36)-(37) ортогональные многочлены могут лишь множителями отличаться от тех, которые строятся по методу Грама-Шмидта.
Квадрат нормы полиномов Лежандра равен
![]()
| < Предыдущая | Следующая > |
|---|