1.7.3. Применение многочленов Чебышева в задаче интерполяции

В следующей теореме решается следующая задача: как следует выбрать узлы интерполяции, чтобы минимизировать погрешность на всем отрезке.

Теорема 1.3. Пусть , тогда наименьшая максимальная абсолютная погрешность интерполяции полиномом Лагранжа на отрезке достигается при выборе в качестве узлов интерполяции нулей функции

Обозначим - корень многочлена . Согласно свойству 4

(28)

Пусть – некоторая система узлов на . Запишем формулу максимальной абсолютной погрешности интерполяции по Лагранжу (формула (10) тз п. п.1.4):

,

Где ,

Как следует из свойства 6:

.

Выберем в качестве узлов точки , определяемые формулой (28). Тогда

.

Отметим, что многочлен имеет одну и ту же степень N+1, что и , один и тот же коэффициент при старшей степени и одни и те же нули на .

Отсюда немедленно следует, что , и соответствующая оценка погрешности:

.

Данная оценка является наилучшей среди всех возможных способов выбора узлов интерполяции.

Замечание. Для оптимальной интерполяции на произвольном конечном отрезке [A;b] предварительно необходимо сделать линейное преобразование:

И преобразовать формулу для нулей функции к следующему виду:

,

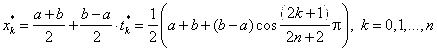Пример 15. Вывести следующую формулу для максимальной абсолютной погрешности интерполяции по Лагранжу на отрезке :

< Предыдущая		Следующая >