1.7.2. Простейшие свойства многочленов Чебышева
1. Многочлены Чебышева ортогональны на отрезке ![]() с весом
с весом ![]() .
.
![]() Рассмотрим интеграл
Рассмотрим интеграл

![]()
В силу ортогональности системы функций ![]() на отрезке
на отрезке ![]() .
.
Вычислим квадрат нормы:
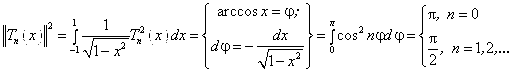 .
. ![]()
2. При четных (нечетных) N многочлен Чебышева Tn(X) содержит только четные (нечетные) степени Х, т. е. является четной (нечетной) функцией.
![]() Доказывается по индукции с помощью рекуррентной формулы (25).
Доказывается по индукции с помощью рекуррентной формулы (25). ![]()
3. Коэффициент при старшей степени Xn многочлена Tn(X) равен 2N-1.
![]() Доказывается по индукции с помощью рекуррентной формулы (25).
Доказывается по индукции с помощью рекуррентной формулы (25). ![]()
4. Многочлен Tn(X) имеет на отрезке ![]() ровно N различных действительных корней, определяемых формулой:
ровно N различных действительных корней, определяемых формулой:

![]() Действительно:
Действительно:
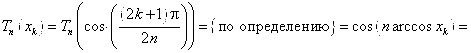

![]()
5. ![]() и достигается в точках экстремума:
и достигается в точках экстремума:
![]() .
.
![]() Из определения (1) следует, что
Из определения (1) следует, что ![]() для любого
для любого ![]() . Очевидно, что
. Очевидно, что
![]() .
. ![]()
6. Многочлен ![]() среди всех многочленов
среди всех многочленов ![]() N-ой степени с коэффициентом при старшей степени An=1 обладает тем свойством, что
N-ой степени с коэффициентом при старшей степени An=1 обладает тем свойством, что
|
|
(26) |
![]() Доказывается от противного: пусть это не так и существует многочлен
Доказывается от противного: пусть это не так и существует многочлен
![]()
Такой, что выполняется противоположное:
|
|
(27) |
Разность (![]() ) – многочлен (N-1)-ой степени, причем в силу (4)
) – многочлен (N-1)-ой степени, причем в силу (4)
![]() .
.
Обозначим ![]() и заметим что, в силу (27)
и заметим что, в силу (27)
|
|
Продолжим рассмотрение разности:

Таким образом, при переходе от точки ![]() к
к ![]() разность (
разность (![]() ) меняет знак. Всего при переходе от точки
) меняет знак. Всего при переходе от точки ![]() к
к ![]() произойдет ровно N смен знака. Отсюда следует, что разность
произойдет ровно N смен знака. Отсюда следует, что разность ![]() имеет на отрезке
имеет на отрезке ![]() ровно N действительных корней (нулей), что противоречит теореме Гаусса, т. к. это многочлен (N-1)-ой степени.
ровно N действительных корней (нулей), что противоречит теореме Гаусса, т. к. это многочлен (N-1)-ой степени. ![]()
Замечание. Благодаря свойству 6 многочлен Чебышева ![]() называется Многочленом, наименее отклоняющимся от нуля.
называется Многочленом, наименее отклоняющимся от нуля.
| < Предыдущая | Следующая > |
|---|