1.6. Интерполяционный полином Ньютона
Пусть ![]() - сетка равноотстоящих узлов. Известны табличные значения
- сетка равноотстоящих узлов. Известны табличные значения ![]() некоторой функции
некоторой функции ![]() .
.
Запишем многочлен Лагранжа в следующем виде:
|
|
(16) |
Введем безразмерную переменную
![]() ,
,
Где H – шаг. Очевидно, что для данной сетки ![]()
![]() .
.
Потребуем выполнения условий совпадения значений полинома с табличными значениями в узловых точках
![]()
![]()
![]()
![]()

Далее по индукции получаем общую формулу для коэффициента
|
|
Заметим, что из определения Q следует, что
|
|
(17) |
Подставляя (17) и формулу для ![]() в (16), получаем:
в (16), получаем:
|
|
(18) |
Формула (18) называется Первой интерполяционной формулой Ньютона или Формулой «интерполирования вперед».
Замечание. Мы получили два различных представления для одного и того же интерполяционного полинома (интерполяционный полином Лагранжа и интерполяционный полином Ньютона). Отметим некоторые очевидные особенности практического применения этих двух видов.
Интерполяционный полином в форме Лагранжа содержит значения ![]() В явном виде. Это удобно, когда надо построить интерполяционный полином по той же сетке, но для другой функции
В явном виде. Это удобно, когда надо построить интерполяционный полином по той же сетке, но для другой функции ![]() . В этом случае достаточно значения
. В этом случае достаточно значения ![]() поменять на
поменять на ![]() .
.
Интерполяционный полином в форме Ньютона (4) содержит значения ![]() неявно (через конечные разности). Однако он удобен, когда для той же функции
неявно (через конечные разности). Однако он удобен, когда для той же функции ![]() необходимо увеличить число узлов N для повышения точности. В этом случае к исходной записи многочлена достаточно добавить несколько таких же членов, если в запасе остались неиспользованными узлы сетки.
необходимо увеличить число узлов N для повышения точности. В этом случае к исходной записи многочлена достаточно добавить несколько таких же членов, если в запасе остались неиспользованными узлы сетки.
Кроме того, на практике обычно формулу (18) используют для интерполяции в точках X, близких к точке X0. В этом случае Q мало и требуется небольшое число членов ряда для достижения нужной точности.
В то же время многочлен в форме Лагранжа дает, как правило, наибольшую максимальную абсолютную погрешность в точках, близких к краям отрезка ![]() .
.
Приведем простейшие частые случаи интерполяции по Ньютону:
1) Линейная интерполяция, ![]() :
:
![]() .
.
2) Квадратичная интерполяция, ![]() :
:
![]() .
.
Пример 11. Задана таблица интерполяции в равноотстоящих узлах.

Используя интерполяцию по Ньютону, вычислить приближенно значение ![]() .
.
![]() Составляем конечные разности и дополняем таблицу столбцами конечных разностей
Составляем конечные разности и дополняем таблицу столбцами конечных разностей ![]() и
и ![]() . Обнаруживаем, что вторые конечные разности постоянны. Следовательно,
. Обнаруживаем, что вторые конечные разности постоянны. Следовательно, ![]() и достаточно ограничиться многочленом 2-го порядка:
и достаточно ограничиться многочленом 2-го порядка:
![]() .
.
Используя первую строку таблицы и значение ![]() , получаем
, получаем
![]() .
. ![]()
Погрешность интерполяционной формулы Ньютона.
Нам известна теоретическая оценка погрешности интерполяции в точке по Лагранжу
|
|
(5) |
![]() .
.
Преобразуем многочлен ![]() для случая равноотстоящих узлов:
для случая равноотстоящих узлов:
Поскольку ![]() , то
, то
![]() .
.
Т. о. для оценки погрешности в точке получаем:
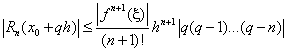
Или
|
|
(19) |
Где
![]() .
.
Из формулы (19) следует оценка для максимальной абсолютной погрешности интерполяционной формулы Ньютона на всем отрезке
|
|
(20) |
![]() Пример 12. Показать, что из формулы (20) следует более простая, но завышенная оценка
Пример 12. Показать, что из формулы (20) следует более простая, но завышенная оценка
|
|
(21) |
Подчеркивающая степенную зависимость точности интерполяции от шага H.
![]() Для вывода (21) показать сначала, что
Для вывода (21) показать сначала, что
![]() .
.
Доказательство провести по индукции: ![]() и т. д.
и т. д. ![]()
![]() Пример 13. Каков должен быть шаг H таблицы интерполяции для функции
Пример 13. Каков должен быть шаг H таблицы интерполяции для функции ![]() , чтобы при квадратичной интерполяции на отрезке
, чтобы при квадратичной интерполяции на отрезке ![]() погрешность не превосходила
погрешность не превосходила ![]() ?
?
![]() Ответ:
Ответ: ![]() . Использовать оценку (21).
. Использовать оценку (21). ![]()
![]() Пример 14. Вывести Вторую интерполяционную формулу Ньютона (формулу «интерполирования назад»).
Пример 14. Вывести Вторую интерполяционную формулу Ньютона (формулу «интерполирования назад»).
![]() Ищем интерполяционный многочлен в виде:
Ищем интерполяционный многочлен в виде:
|
|
(22) |
Накладывая условия
![]() ;
;
Аналогично выводу формулы (18), получим общее выражение для ![]() :
:
![]()
Вводя безразмерную переменную
![]()
И преобразуя (22), получаем выражение для Второй формулы Ньютона:
|
|
(23) |
Для погрешности интерполяции получаем соответственно:
![]()
![]()
В формуле (23) используются конечные разности которые образуются в последних строках таблицы.
Замечание. Множество различных видов интерполяционных полиномов не исчерпывается приведенными тремя видами. Результат зависит от двух факторов: от вида сетки (равномерная или неравномерная) и от выбора базового узла ![]() . Например для равномерной сетки и при выборе базового узла
. Например для равномерной сетки и при выборе базового узла ![]() в центральной части отрезка
в центральной части отрезка ![]() используются так называемые центральные разности. В результате получаются еще 3 вида записи интерполяционных полиномов: формулы Гаусса, Стирлинга и Бесселя [1].
используются так называемые центральные разности. В результате получаются еще 3 вида записи интерполяционных полиномов: формулы Гаусса, Стирлинга и Бесселя [1].
| < Предыдущая | Следующая > |
|---|
