1.5. Конечные разности и их свойства

Пусть задана равномерная сетка узлов . Обозначим – множество узловых точек.

Определение. Величина

Называется Конечной разностью первого порядка (или разностью «на шаг вперед»).

……………………..

- конечная разность M-го порядка.

Свойства конечных разностей.

1. Операторы - линейные операторы.

Пусть - произвольные табличные значения.

Доказательство проводим по индукции. Вначале проверяем утверждение для M=1.

Оператор линейный.

Далее пусть - линейный оператор. Покажем, что и линейный.

2. линейно выражается через значения .

По индукции. Для M=1 и 2 уже доказано в определении. Пусть утверждение справедливо для , где M>2, тогда

Пример 9. Выразить явно через .

Самостоятельно.

3. Операторы и - перестановочные, т. е.

.

1) Докажем, что операторы и перестановочные.

.

В обратном порядке:

.

То же самое получим, действуя в обратном порядке.

4. Рассмотрим сетку , в ней введен дополнительный узел . Пусть функция Тогда справедливы следующие формулы:

.	(14)
.	(15)

Пусть M=1. Тогда

Где H – приращение аргумента.

M=2.

(1).

Уравнение (15) является частным случаем уравнения (14) при .

5. Для сетки Xn рассмотрим полином M-го порядка

.

Таким образом для полинома -го порядка конечные разности -го порядка постоянны, а конечные разности порядков, больших, чем , равны нулю.

Пример 10. Пусть .

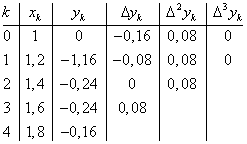
Рассмотрим сетку узлов Составить таблицу конечных разностей.

Заметим, что вторые разности постоянны в соответствии со свойством 5. Кроме того, верхняя строка таблицы относится к конечным разностям в точке X0.

Замечание. Справедливо и обратное к свойству 5 утверждение: если для некоторой функции M-ные конечные разности постоянны при любом выборе шага, то это означает, что .

< Предыдущая		Следующая >