1.2. Распространение ошибок округления в арифметических операциях

1) Операции сложения и вычитания.

Пусть , . Тогда

, где .

Поскольку , то ,

Т. е. при сложении чисел предельные абсолютные ошибки складываются.

Не трудно убедиться, что такое же правило справедливо и для разности.

2) Операция умножения.

Пусть

,

Где , тогда

,

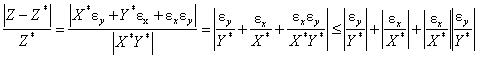Следовательно,

,

Т. е. .

Если последнее слагаемое имеет второй порядок малости по сравнению с первыми двумя, то им можно пренебречь. В этом случае получаем более простое правило: при умножении относительные максимальные ошибки приближенно складываются.

3) Операция деления.

Пусть , , .

Пример 4. Показать, что справедливо следующее правило:

.

Самостоятельно .

4) Погрешность вычисления функции при неточном задании аргументов.

Рассмотрим для определенности функцию двух переменных, непрерывно-дифференцируемую в области GR2. Пусть приближенное значение точки, причем замкнутый прямоугольник

Содержит обе указанные точки.

Пусть , , , .

По формуле конечных приращений Лагранжа имеем:

,

Где - некоторая точка замкнутого прямоугольника .

Отсюда, оценивая обе части равенства по модулю, получим

.

Если известны оценки: , , где (, то максимальная абсолютная ошибка вычисления функции:

.

< Предыдущая		Следующая >