1.3. Понятие близости в метрическом пространстве

Определение 1. Множество X элементов произвольной природы (не обязательно числовое множество) называется Метрическим пространством, если любой паре элементов поставлено в соответствие число , (метрика, или расстояние) в соответствии с аксиомами:

А1. тогда и только тогда, когда X=y.

А2. .

А3. – неравенство треугольника.

Определение 2. Говорят, что последовательность элементов метрического пространства X сходится к элементу , если .

Определение 3. Последовательность элементов метрического пространства X называется Фундаментальной, если .

Определение 4. Метрическое пространство X называется Полным, если любая фундаментальная последовательность его элементов сходится к некоторому элементу этого пространства.

Замечания.

Не любое метрическое пространство является полным.

Например, множество всех рациональных чисел с метрикой

Не является полным, т. к., скажем, последовательность 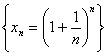- фундаментальная, но 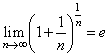- иррациональное число.

Сходимость большинства итерационных процессов удается доказать только в полном метрическом пространстве, следовательно, полнота играет важную роль в числовом анализе.

Определение 5. Множество X называется Нормированным линейным пространством, если

Оно является линейным пространством, т. е. в нем определены операции сложения элементов и умножения элемента на число с известными свойствами.

Любому элементу поставлено в соответствие число (норма X), удовлетворяющее аксиомам:

А1. ,

А2.

А3. – неравенство треугольника.

Замечание. Любое нормированное линейное пространство X можно считать метрическим, если ввести метрику по формуле

, (1)

Если последовательность нормированного пространства X сходится в смысле метрики (1), то говорят о сходимости по норме пространства X.

Нетрудно убедиться, что для метрики (1) выполняются все аксиомы метрики.

Приведем некоторые примеры классов функций и соответствующих линейных пространств.

Пример 5. Множество всех функций, заданных на отрезке [A, b] и имеющих на нем непрерывные производные до K - го порядка включительно, называется классом .

Пример 6. При K=0 получаем класс - множество непрерывных на отрезке [A, b] функций.

Если на ввести норму по формуле

,

(2)

то получим линейное нормированное пространство C[A, b] (операции сложения и умножения на число вводятся обычным образом F+g=f(X)+g(X), ).

Аксиомы А1, А2 – очевидно, выполняются. В справедливости А3 нетрудно также убедиться с помощью свойств модуля и теоремы Вейерштрасса.

Замечания.

Норму в классе можно ввести не единственным образом.

Например,

.

Сходимость последовательности по норме (2) – это равномерная сходимость:

.

Пространство C[A, b] с нормой (2) является полным в силу теоремы мат. анализа: Равномерно сходящаяся последовательность в замкнутой области сходится к непрерывной функции.

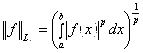
Пример 7. Множество всех функций, P-я степень модуля которых интегрируема на отрезке [A, b], называется линейным нормированным пространством , если на нем введена норма по формуле

.

(3)

Сходимость по норме (3) называется Сходимостью в среднем (при P=2 - среднеквадратичная сходимость).

Замечание. Пусть , тогда .

, .

Отсюда следует, что из сходимости последовательности по норме C следует ее сходимость по норме , но не наоборот.

< Предыдущая		Следующая >