1.1. Численные методы в теории приближений. Структура погрешности в численном анализе

Рассмотрим основные источники погрешностей, возникающих в численном анализе.

1. Погрешности математической модели.

Любая задача есть модель какого-то явления. Всякая модель – это объект более простой, чем реальный. Модель – приближенное описание реального объекта, т. е. содержит погрешности.

2. Погрешности исходных данных.

Данные могут оказаться неточными в результате неточных измерений или ввода в компьютер таких констант как π, е и др.

3. Погрешности метода решения.

Численные методы заменяют задачу на близкую. Например, вместо интегрирования – суммирование, вместо дифференцирования – вычисление конечно разностного отношения и т. д. В результате вместо точного решения исходной задачи получаем приближенное решение преобразованной задачи.

4. Погрешности округлений при выполнении арифметических операций.

В рамках численных методов погрешности 1 и 2 считаются неустранимыми. Погрешность метода обычно оценивается в норме того метрического пространства, в котором действуют операторы преобразованной задачи. Чаще всего алгоритм решения устроен как итерационный процесс. Поэтому возникает проблема сходимости этого процесса к некоторому решению – приближенному решению исходной задачи и вопрос о близости полученного решения к точному решению исходной задачи.

Рассмотрим подробнее пункт 4 – ошибки округления.

Ошибки округления связаны с устройством арифметического процессора на ЭВМ, имеющего конечную разрядность. Чтобы разобраться в этом вопросе, рассмотрим две Основные формы записи чисел.

1) Запись числа в позиционной системе счисления:

,

Где A – основание позиционной системы, A{2,8,16,10,…},

.

Пример 1. Пусть A =10. Расшифровать десятичное число X= 27,135

.

Определение 1. Значащими называются все цифры числа X, записанного в позиционной системе, начиная с первой слева отличной от нуля.

Пример 2. В записи числа X = 0,006071 значащими являются цифры 6,0,7,1.

2) Нормализованная форма записи числа (запись числа в арифметическом процессоре «с плавающей запятой»):

,

Где F – мантисса числа X, удовлетворяющая условию , А - основание системы счисления (А=2,8,10 и т. д.), L – порядок числа, ,

,

- цифра в K-ом разряде мантиссы (дробного числа), , K=2,3,… , 0< F1<A, T – число используемых значащих цифр (характеристика вычислительного устройства).

Пример 3. Пусть X = 0,03045 в десятичной системе. Записать число X в нормализованной форме.

.

Если вводимое в ЭВМ число X (или полученное на каком либо этапе вычислительного процесса) имеет число значащих цифр мантиссы, превышающее значение T, то происходит так называемое округление числа. В компьютерах обычно реализовано Симметричное округление по следующему правилу: если в старшем из отбрасываемых разрядов стоит цифра меньшая пяти, то содержимое сохраняемых разрядов числа не изменяется. В противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа. Кратко это правило формулируют так: округление До ближайшего целого.

Существуют и другие правила округления, осуществляемые по решению пользователя ЭВМ. Например, в пакете MATLAB реализовано четыре специальные команды округления чисел: Fix, Ceil, Floor, Round. Подробно эти и другие способы округления чисел обсуждаются на семинарских занятиях и лабораторных работах.

Ошибка округления, будучи внесена на каком либо этапе вычислительного процесса, начинает распространяться во всех последующих операциях. Таким образом, в конечный результат будет внесена результирующая ошибка округления.

Введем основные понятия, связанные с погрешностью чисел.

Пусть - приближенное представление числа X, т. е. , где - погрешность.

Определение 2. Величина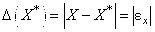

Называется Абсолютной погрешностью представления числа X с помощью числа .

Максимально возможное значение , т. е. число , удовлетворяющее неравенству , называется Максимальной или Предельной Абсолютной погрешностью (Ошибкой).

Определение 3. Величина, равная

,

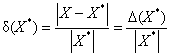Называется Относительной ошибкой представления числа X числом .

Если , то число называется Максимальной предельной относительной ошибкой.

Определение 4. Значащая цифра αJ числа X, записанного в позиционной системе, называется Верной в широком смысле, если выполняется условие Δ(X*)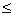A J и Верной в узком смысле, если выполняется условие Δ(X*)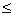0,5*A J.

В дальнейшем курсе будет использоваться главным образом понятие верной цифры в широком смысле.

< Предыдущая		Следующая >