21. Смешанное произведение

Смешанным произведением тройки векторов , и называется число, равное скалярному произведению вектора на векторное произведение 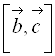. Если рассматриваемые векторы , и некомпланарны, то векторное произведение 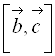есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор , то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов , и , и его высоты, т. е. объему этого параллелепипеда.

Таким образом, смешанное произведение векторов 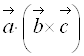(которое обозначается 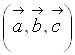) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах , и .

Знак произведение положителен, если векторы , и , образуют правую тройку векторов, т. е. вектор направлен так, что кратчайший поворот от к виден из его конца совершающимся против часовой стрелки.

Из геометрического смысла смешанного произведения непосредственно следует необходимое и достаточное условие некомпланарности векторов , и : Для того, чтобы векторы , и были некомпланарными необходимо и достаточно, чтобы их смешанное произведение было отлично от нуля.

Если , и , то:

,

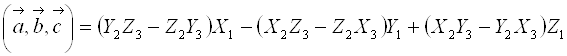Или в свернутой форме:

.

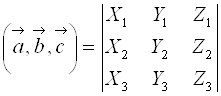Справедливы следующие Свойства смешанного произведения векторов:

1. Смешанное произведение не меняется при циклической перестановке его сомножителей ;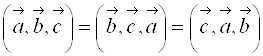

2. При перестановке двух соседних множителей смешанное произведение меняет свой знак на противоположный .

Контрольные вопросы к лекции №4

1. Понятие скалярной величины.

2. Понятие векторной величины.

3. Понятия единичного вектора и нулевого вектора.

4. Модуль вектора, формула расстояния между двумя точками.

5. Понятие коллинеарности векторов.

6. Понятие компланарности векторов.

7. Понятие проекции вектора на ось.

8. Линейные операции над векторами.

9. Скалярое произведение векторов.

10. Векторное произведение векторов.

11. Смешанное произведение векторов.

< Предыдущая		Следующая >