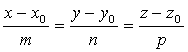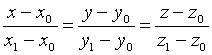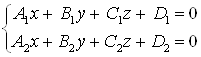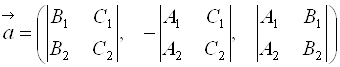22. Лекция 5. Прямая
Основные понятия:
Векторное параметрическое уравнение прямой; параметрические уравнения прямой в пространстве; канонические уравнения прямой; направляющий вектор прямой.
Прямая ![]() в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой).
в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой).
 Пусть задана такая точка
Пусть задана такая точка ![]() и вектор
и вектор ![]() (Рис. 5.1).
(Рис. 5.1).
Если ![]() ‑ произвольная текущая точка прямой
‑ произвольная текущая точка прямой ![]() , то вектор
, то вектор ![]() коллинеарен вектору
коллинеарен вектору ![]() и их соответствующие координаты пропорциональны.
и их соответствующие координаты пропорциональны.
|
|
(5.1) |
Этим соотношениям удовлетворяют координаты любой точки прямой ![]() и только этой прямой. Равенства (5.1) называются Каноническими уравнениями прямой в пространстве.
и только этой прямой. Равенства (5.1) называются Каноническими уравнениями прямой в пространстве.
Обозначим ![]() радиус-вектор точки
радиус-вектор точки ![]() ,
, ![]() ‑ радиус-вектор точки
‑ радиус-вектор точки ![]() . Тогда:
. Тогда:
|
|
(5.2) |
В силу коллинеарности векторов ![]() и
и ![]() существует число
существует число ![]() такое, что
такое, что ![]() . Тогда из (5.2) получим векторное параметрическое уравнение прямой:
. Тогда из (5.2) получим векторное параметрическое уравнение прямой:
|
|
(5.3) |
В координатной форме уравнение (5.3) равносильно трем уравнениям:
|
|
(5.4) |
Которые называются Параметрическими уравнениями Прямой в пространстве.
Исключая из уравнений (5.4) параметр ![]() , легко перейти к каноническим уравнениям прямой (5.1).
, легко перейти к каноническим уравнениям прямой (5.1).
Обратный переход от (5.1) к (5.4) осуществляют, приравнивая каждое из трех соотношений (5.1) к ![]() . При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
. При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
Пусть заданы точки ![]() и
и ![]() . Составим уравнение прямой, проходящей через заданные точки, пользуясь
. Составим уравнение прямой, проходящей через заданные точки, пользуясь
рис. 5.1.
Очевидно, что в этом случае направляющим вектором прямой ![]() будет вектор
будет вектор ![]() . Используя (5.1), получаем искомые уравнения в виде:
. Используя (5.1), получаем искомые уравнения в виде:
|
|
(5.5) |
Прямую ![]() в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии
в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии ![]() в общем виде:
в общем виде:
|
|
(5.6) |
Система двух уравнений первой степени (5.6) определяет прямую линию при условии, что нормальные векторы ![]() и
и ![]() неколлинеарны. Только в этом случае плоскости будут пересекаться. Уравнения (5.6) носят название «Общее уравнение прямой в пространстве».
неколлинеарны. Только в этом случае плоскости будут пересекаться. Уравнения (5.6) носят название «Общее уравнение прямой в пространстве».
Чтобы перейти от общих уравнений прямой (5.6) к ее каноническим уравнениям (5.1), нужно на прямой найти какую-нибудь точку ![]() и определить ее направляющий вектор
и определить ее направляющий вектор ![]() .
.
Точку ![]() находят, давая произвольное значение одной из переменных
находят, давая произвольное значение одной из переменных ![]() ,
, ![]() или
или ![]() . Решая систему (5.6), получают значения оставшихся двух переменных.
. Решая систему (5.6), получают значения оставшихся двух переменных.
Направляющий вектор ![]() параллелен линии пересечения плоскостей (5.6) и, следовательно, перпендикулярен обоим нормальным векторам плоскостей:
параллелен линии пересечения плоскостей (5.6) и, следовательно, перпендикулярен обоим нормальным векторам плоскостей:
![]() .
.
Поэтому в качестве ![]() можно взять вектор:
можно взять вектор:

|
|
(5.7) |
| < Предыдущая | Следующая > |
|---|