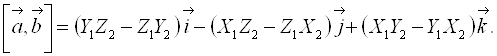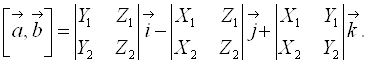20. Векторное произведение

Векторным произведением вектора на вектор называется вектор 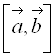, длина и направление которого определяется условиями:

1. 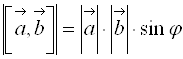, где ‑ угол между и ;

2. 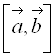перпендикулярен каждому из векторов и ;

3. 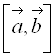направлен так, что кратчайший поворот от к виден из его конца совершающимся против часовой стрелки.

Векторное произведение обладает следующими свойствами:

1. ;

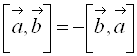2. ;

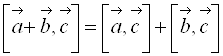3. ;

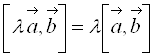4. Векторное произведение равно нулю (нуль вектору) тогда и только тогда, когда и коллинеарны. В частности, 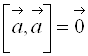для любого вектора ;

5. Если и неколлинеарны, то модуль векторного произведения равен площади параллелограмма построенного на этих векторах, как на сторонах.

Из первых трех свойств следует, что векторное умножение суммы векторов на сумму векторов подчиняется обычным правилам перемножения многочленов. Надо только следить за тем, чтобы порядок следования множителей не менялся.

Основные орты перемножаются следующим образом:

.

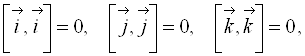
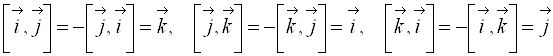Если и , то c учетом свойств векторного произведения векторов, можно вывести правило вычисления координат векторного произведения по координатам векторов-сомножителей:

.

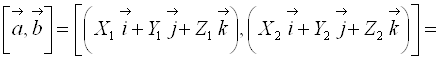
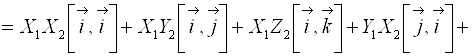
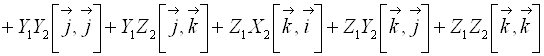Если принять во внимание полученные выше правила перемножения ортов, то:

(4.11)

Более компактную форму записи выражения для вычисления координат векторного произведения двух векторов можно построить, если ввести понятие определителя матрицы.

Рассмотрим частный случай, когда вектора и принадлежат плоскости , т. е. их можно представить как и .

Если координаты векторов записать в виде таблицы следующим образом: 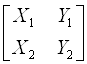, то можно сказать, что из них сформирована квадратная матрица второго порядка, т. е. размером , состоящая из двух строк и двух столбцов. Каждой квадратной матрице ставится в соответствие число, которое вычисляется из элементов матрицы по определенным правилам и называется определителем. Определитель матрицы второго порядка равен разности произведений элементов главной диагонали и побочной диагонали:

.

В таком случае:

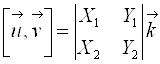
Абсолютная величина определителя, таким образом, равна площади параллелограмма, построенного на векторах и , как на сторонах.

Если сравнить это выражение с формулой векторного произведения (4.7), то:

(4.12)

Это выражение представляет собой формулу для вычисления определителя матрицы третьего порядка по первой строке.

Таким образом:

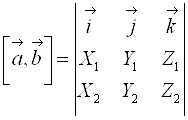
Определитель матрицы третьего порядка вычисляется следующим образом:

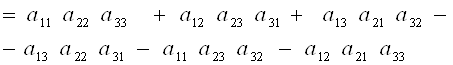
И представляет собой алгебраическую сумму шести слагаемых.

Формулу для вычисления определителя матрицы третьего порядка легко запомнить, если воспользоваться Правилом Саррюса, которое формулируется следующим образом:

· Каждое слагаемое является произведением трех элементов, расположенных в разных столбцах и разных строках матрицы;

· Знак “плюс” имеют произведения элементов, образующих треугольники со стороной, параллельной главной диагонали;

· Знак “минус” имеют произведения элементов, принадлежащих побочной диагонали, и два произведения элементов, образующих треугольники со стороной, параллельной побочной диагонали.

< Предыдущая		Следующая >