19. Скалярное произведение

Скалярными произведением двух векторов и называется число, равное произведению их длин на косинус угла между ними: .

Скалярное произведение обладает следующими свойствами:

1. ;

2. ;

3. ;

4. Если и ‑ ненулевые векторы, то Тогда и только тогда, когда эти векторы перпендикулярны. Если , то угол между и - острый, если , то угол - тупой;

5. Скалярный квадрат вектора равен квадрату его длины, т. е. .

Следовательно, .

Геометрический смысл скалярного произведения: скалярное произведение вектора на единичный вектор равно проекции вектора на направление, определяемое , т. е. .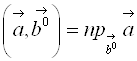

Из определения скалярного произведения вытекает следующая таблица умножения ортов :

.

Если векторы заданы своими координатами и , т. е. , , то, перемножая эти векторы скалярно и используя таблицу умножения ортов, получим выражение скалярного произведения 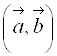через координаты векторов:

.

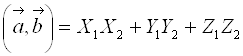< Предыдущая		Следующая >