5.3. Разные задачи

Предварительно изучите по учебнику Г. М. Фихтен-гольца главу XII, п° 208.

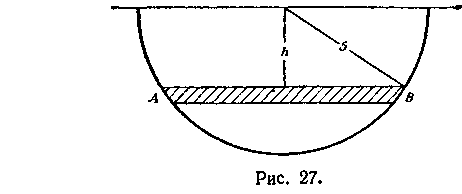
611. Найти давление на полукруг, вертикально погруженный в жидкость, если его радиус равен 5 см, а верхний диаметр лежит на свободной поверхности воды

Решение. Давление жидкости на дно сосуда равно весу вертикального столба жидкости с основанием в I см, находящегося над дном. Объем столба, имеющего в основании единицу площади, а высоту h, равен А. Поэтому давление на глубине h будет:

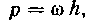
где со — вес кубической единицы этой жидкости.

Чтобы вычислить давление на вертикальную поверхность, воспользуемся тем фактом, что в каждой точке давление во все стороны одинаково. На рисунке 27 изображена вертикальная поверхность. Давление на полосу AB, содержащуюся между двумя весьма близкими горизонталями, приближенно равно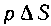, где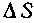—площадь этой полоски. Зная это элементарное давление, найдем искомое давление Р:

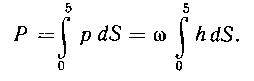
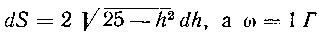
Так как, то

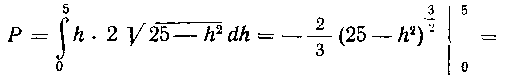
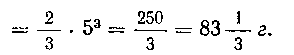
612. Вычислить давление на треугольник, имеющий основание b сму высоту h сму если вершина треугольника лежит на поверхности воды, а высота его расположена вертикально.

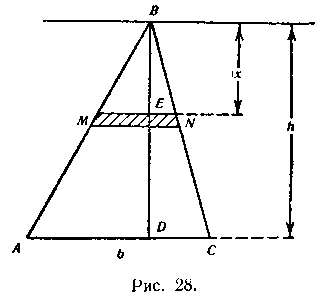
Решение. На рисунке 28 изображен данный треугольник, погруженный в воду. Берем произвольную полоску MN, находящуюся на глубине х см. Ее длина легко определяется из подобия треугольников ВАС и BMN. Принимая (приближенно) эту полоску за прямоугольник, найдем ее площадь: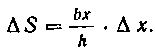Отсюда

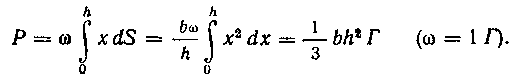
613. Вычислить давление жидкости на боковые стенки кругового цилиндра, высота которого равна h см, а радиус основания г см, удельный вес жидкости равен d.

614. Вычислить давление, испытываемое треугольником, высота которого равна h см, основание равно Ь см> если он погружен в воду таким образом, что основание его лежит на поверхности воды, а высот# направлена вертикально вниз.

615. Вычислить давление воды на щит, имеющий форму трапеции, погруженный в воду вертикально. Верхнее основание, равное а м, лежит на поверхности воды, нижнее основание равно b м, высота щита равна h м.

616. Конец трубы, погруженной горизонтально в воду, закрыт заслонкой. Определить давление, испытываемое этой заслонкой, если ее диаметр равен 60 сму а центр ее находится на глубине 15 м под водой.

617. Сжатие винтовой пружины пропорционально приложенной силе. Вычислить работу, производимую при сжатии пружины на 4 сму если для сжатия ее на I см нужно приложить силу в I кг.

Решение. Обозначим через х сжатие пружины. Тогда, согласно закону Гука, F = kx% где k — постоянная, характеризующая материал пружины. Для данного случая

Предполагая, что F выражена в килограммах, ах—в метрах, найдем произведенную работу А:

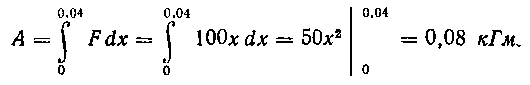
€18. Работа, которую необходимо затратить, чтобы поднять тело от одной высоты до другой, выраженная в килограммометрах, равна произведению веса тела в килограммах на высоту поднятия, выраженную в метрах. Вычислить работу, которую необходимо затратить, чтобы выкачать воду из цилиндрической цистерны, радиус которой равен a M9 а высота — Ъ м.

Решение. Разобьем объем цистерны плоскостями, параллельными основанию и находящимися друг от друга на расстоянии А х. Вычислим объем полученного элементарного цилиндра:

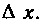
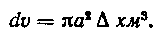
dv = яа* А хм3.

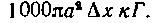
Вес воды в этом объеме будет равен I ОООяа* tax кГ. Элементарная работав, затраченная для поднятия этой массы, находящейся на глубине хм, равна:

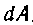
dA = ЮООяа2 А х-хкГм.

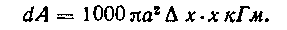
ь ь

Отсюда искомая работа равна:

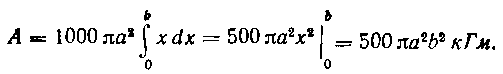
А «в 1000 я a2 f х dx = 500 яа2*21 — 500 па2Ь2 кГм.

о о

619. Вычислить работу на преодоление силы тяжести, которую необходимо затратить, чтобы выкачать воду из резервуара, имеющего форму конуса, обращенного вершиной вниз Высота конуса Hy радиус R.

620 Какую работу надо затратить, чтобы насыпать кучу песка конической формы с радиусом 1,2 м и высотой I Mf если удельный вес песка равен 2?

621. Шар радиуса R9 изготовленный из материала, плотность которого P= 1г/см3у погружен в воду так, что касается поверхности. Какую работу нужно произвести, чтобы вытащить шар из воды?

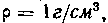
622. Конус, радиус основания которого R = AOcMy высота H = 20сму плавает на поверхности воды сверху. Плотность материала, из которого сделан конус, р = = 0,9 е/см3. Какую работу нужно затратить, чтобы погрузить конус полностью в воду?

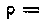
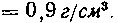
623. Вычислить работу, производимую при растягивании пружины на 0,05 му если известно, что сила, которая требуется для растяжения пружины, пропорциональна удлинению х пружины и что для удлинения пружины на 0,01 м требуется сила, равная I кГ.

624. Вычислить работу, необходимую для того, чтобы выкачать воду из полусферического сосуда, радиус которого Rm.

625. Вычислить давление ртути, наполняющей стакан, на боковые стенки стакана, если высота стакана равна 12 см, диаметр основания равен 8 см, удельный вес ртути равен 13,6.

Дополнительные задачи к главе V

626. Найти центр тяжести полуокружности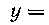

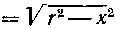
627. Найти центр тяжести полукруга, ограниченного полуокружностью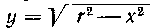И осью Ox.

628. Найти координаты центра тяжести фигуры, ограниченной дугой астроиды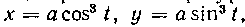Расположенной в первом квадранте, и осями координат.

629. Найти декартовы координаты центра тяжести фигуры, ограниченной кардиоидой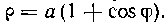

630. Найти декартовы координаты центра тяжести фигуры, ограниченной правой петлей лемнискаты Бернулли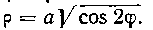

< Предыдущая		Следующая >