5.2. Вычисление координат центра тяжести плоских кривых и плоских тел. Теоремы Гюльдена
Предварительно изучите по учебнику Г. М. Фихтен-гольца главу XII, п° 206, 207. При решении задач рекомендуется помнить, что если кривая расположена симметрично относительно некоторой прямой, то центр тяжести кривой лежит на этой прямой.
592. Найти центр тяжести дуги цепной линии:
содержащейся между точками, для которых х = — а х = а.
Решение. Так как рассматриваемая дуга расположена симметрично относительно оси Oyt то центр тяжести дуги лежит на оси Oy и, следовательно,
Найдем ординату
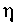, пользуясь формулой
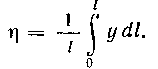
Так как
и, следовательно,
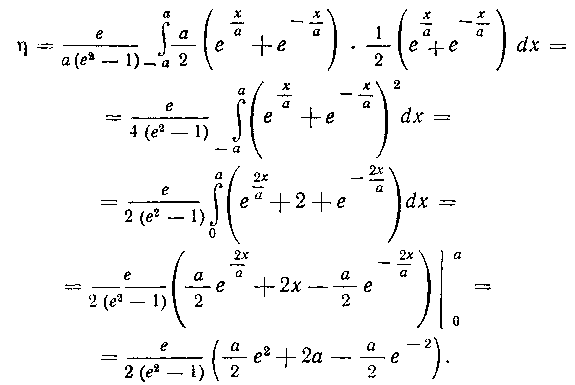
593. Найти центр тяжести одной арки циклоиды:
Решение. Так как арка циклоиды расположена симметрично относительно прямой х = па, то центр тяжести дуги циклоиды лежит на этой прямой и, следовательно,
Ордината центра тяжести будет: ? ( ~ е [а I а
Ц - - Ie _L_£
1 a(e*~-\)Ja 2 \ f
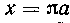
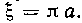
I = Jt а.
Найдем ординату центра тяжести по формуле:
Длина дуги одной арки циклоиды равна 8а (см. задачу
Найдем ординату центра тяжести:
594. Найти центр тяжести дуги кривой»
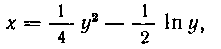
содержащейся между точками, для которых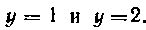
Решение. Найдем
(см. задачу 491).
Найдем абсциссу центра тяжести: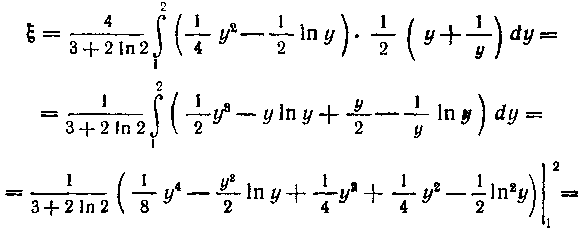 
3 + 2 In 2
4
Найдем ординату центра тяжести:
2
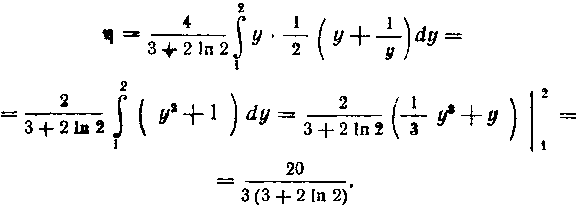
595. Найти центр тяжести однородной треугольной пластинки.
ч
3 (3 + 2 In 2)
Решение. Разбиваем данную пластинку прямыми, параллельными одной из сторон, на бесконечно тонкие полоски. Центр тяжести каждой полоски находится в ее середине и лежит, таким образом, на медиане, а следовательно, и центр тяжести всей треугольной пластинки лежит на этой медиане. Так как это рассуждение применимо к любой стороне, то центр тяжести треугольника находится в точке пересечения его медиан.
Тот же результат получаем вычислением. Площадь полоски, отстоящей на расстояние х от данной стороны
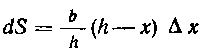
Ь, равна dS = —(h—х) А я, где А —высота, опущенная h
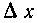
на эту сторону, а Дл; — ширина полоски, следовательно, расстояние центра тяжести от этой стороны равно: н н
I*= — [ xdS — Г— (h—х) xdx =
SJ bh J h 9
A1 \ 2 3 J I о 3 Таким образом, центр тяжести треугольника находится на расстоянии, равном — высоты от соответствующей
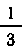
стороны, т. е. в точке пересечения его медиан, ибо это— е&инственная точка, обладающая таким свойством.
596. Найти центр тяжести площади, ограниченной осью Ox и одной полуволной синусоиды
Решение. Так как площадь одной полуволны синусоиды расположена симметрично относительно прямой
, то центр тяжести лежит на этой прямой и, сле
довательно, . Ордината центра тяжести находится
по формуле
Так как
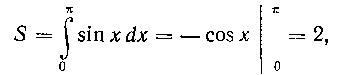
то
Итак, центр тяжести данной площади находится в точке
597. Найти координаты центра тяжести площади, ограниченной параболами
Решение. Данные параболы, пересекающиеся в точках О (0, 0) и А (а; а), ограничивают площадь, расположенную симметрично относительно биссектрисы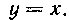
Следовательно, центр тяжести данной площади лежит на биссектрисе, а отсюда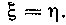
Так как площадь ограничена двумя кривыми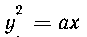
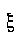
и, то абсцисса центра тяжести площади на-
ходится по формуле:
найдем:
точке
598. Найти центр тяжести площади, ограниченной осью абсцисс и одной аркой циклоиды:
Таким образом, центр тяжести площади находится в
Решение. Данная площадь расположена симметрично относительно прямой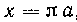
, следовательно, центр тяжести ее находится на этой прямой и отсюда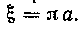
Найдем ц по формуле. Площадь S данной
фигуры была вычислена (см.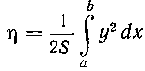
Задачу 467):Сле
довательно,
Центр тяжести данной площади находится в точке 
599. Пользуясь теоремой Гюльдена, вычислить поверхность тора, образованного вращением круга радиуса а вокруг оси, расположенной в его плоскости и отстоящей от центра его на расстояние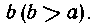
Решение. Так как длина данной окружности равна 
, а длинаокружности, описанной центром тяжести ее, равна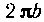
, то поверхность тора по первой теореме Гюльдена равна:
600. Пользуясь теоремой Гюльдена, вычислить объем и боковую поверхность прямого кругового конуса.
Решение. Боковая поверхность конуса с высотой
, образующей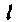
И радиусом основания
Получается при вращении гипотенузы длиной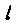
Вокруг катета длиной
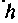. Центр тяжести гипотенузы находится на ее середине и
удален от оси вращения на
. Поэтому по первой теореме Гюльдена боковая поверхность равна:
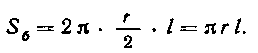
Площадь треугольника равна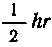
, центр тяжести его, находясь на пересечении медиан, отстоит от катета А на расстояние, равное
Высоты, опущенной на этот катет, т. е.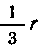
, следовательно, по второй теореме Гюльдена объем конуса равен:
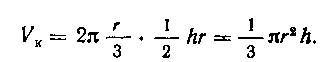
601. На цилиндре, имеющем 6 см в диаметре, кругом вдоль поверхности вырезан канал, имеющий поперечным сечением равносторонний треугольник со стороной в 0,5 сж. Вычислить объем срезанного материала.
Решение. Искомый объем есть объем тела, получаемого при вращении равностороннего треугольника со стороной в 0,5 см вокруг оси, параллельной основанию и удаленной от него на 3 ел, причем вершина лежит между основанием и осью (рис. 26).
Высота треугольника равна
площадь его равна
Расстояние центра тяжести от оси ОС = OA — AC =
(AC равно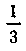
высоты). По второй теореме Гюльдена имеем:
602. Длина одной арки циклоиды
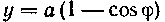Равна
А поверхность, образуемая вращением ее вокруг оси Oxt равна
. Вычислить поверхность, образуемую вращением той же арки циклоиды вокруг касательной в верхней ее точке.
Решение. Пусть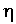
— расстояние центра тяжести от оси Oxi тогда по первой теореме Гюльдена:
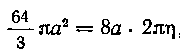, откуда
Наибольшая ордината кривой соответствует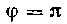
И рав
на 2а, причем касательная в этой точке параллельна оси Ох\ следовательно, расстояние центра тяжести от этой
касательной равно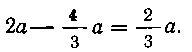
Таким образом, искомая поверхность, образуемая' вращением той же арки циклоиды вокруг касательной в верхней ее точке равна: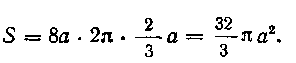
603. Найти центр тяжести дуги, составляющей четверть окружности радиуса
Расположенной в первом квадранте.
604. Найти центр тяжести расположенной в первом квандранте дуги гипоциклоиды x = acosst, у = a sin31.
605. Найти центр тяжести половины площади эллипса, опирающейся на большую ось.
606. Найти центр тяжести площади, заключенной
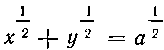
- L - L. L между параболой х2 - J - у2 = а 2 и осями координат.
607. Найти центр тяжести плоской фигуры, ограниченной кривой at/2 = Jc3 и прямой х = а {а > 0).
608. Найти центр тяжести площади, ограниченной кривыми
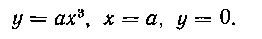
у = ах3, х = а, у = 0.
609. Найти центр тяжести площади, ограниченной эллипсом jc2 -)- 4у2 = 4 и окружностью х2-\- у2 = 4 и расположенной в первом квадранте.
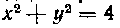
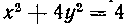
610. Найти центр тяжести фигуры, ограниченной замкнутой кривой у2 = ах3 — х*.
| < Предыдущая | Следующая > |
|---|
