4.I. Вычисление площадей
Внимательно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 193—196. Разберите примеры, приведенные в п° 196. При решении задач с геометрическим содержанием всегда старайтесь сопроводить решение чертежом.
I. Уравнения кривых заданы в декартовой системе координат.
443. Вычислить площадь фигуры, ограниченной дугой параболы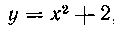
, прямыми X=I9 х — А и отрезком
оси абсцисс.
Решение. В теоретическом курсе показано, что площадь криволинейной трапеции численно равна определенному интегралу
В данном случае (рис. 5) криволинейная трапеция ABDC9 площадь которой мы вычисляем, ограничена параллельными прямыми AB и CD, отрезком прямой AC и отрезком кривой линии BD.
Искомая площадь равна:
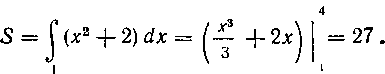
444. Вычислить площадь трапеции, ограниченной дугой параболы и отрезком прямой х = 2.
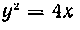
Решение. Из рисунка 6 видно, что искомая площадь расположена симметрично относительно оси абсцисс и, следовательно,
445. Вычислить площадь фигуры, ограниченной кривыми;
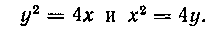
Решение. На рисунке 7 изображена фигура, площадь которой мы должны вычислить. Как видно из рисунка, площадь фигуры OBMAO можно представить как разность двух площадей (пл. OBMPO и OAMPU1 где MP — перпендикуляр, опущенный из точки M на ось Ох).
Найдем координаты точки Al. Решая систему уравнений
получим
Следов ат ельн о,
Легко видеть, что данную задачу можно решить и другим путем. Искомую площадь можно представить в виде разности двух площадей—пл. OAMNO и пл. OBMNO (MN — перпендикуляр, опущенный из точки M на ось Oy):
Тогда
Ясно, что значение площади OBMAO не зависит от способа ее вычисления.
446. Вычислить площадь фигуры, ограниченной петлей кривой: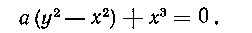
Решение. Из уравнений кривой видно, что она расположена симметрично относительно оси Ох. Следовательно, можно легко вычислить половину искомой площади (см. рис. 8).
Рекомендуем провести самостоятельно подробное исследование кривой.
Записав уравнение кривой в виде
легко найдем точки пересечения кривой с осью Ох, положив у = 0. Мы получим.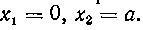
Учитывая все сказанное, окончательно найдем:
447. Вычислить площадь фигуры, ограниченной синусоидой w
И осью Ох, если
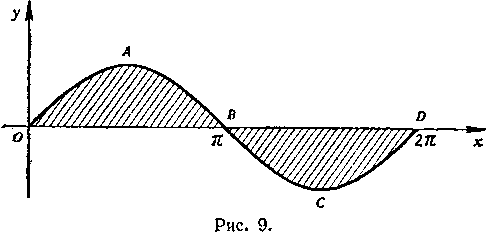
Вся площадь петли равна:
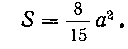
Решение. Из рисунка 9 видно, что искомая площадь на сегменте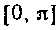
Расположена над осью Ох, а на сегменте
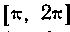Под осью Ох. Следовательно, достаточно вычислить площадь, ограниченную полуволной синусоиды на отрезке
|, и удвоить полученный результат:
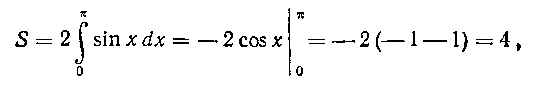
448. Найти всю площадь фигуры, ограниченной кривыми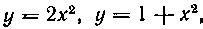
, прямыми X = 3, X = —2 и осью Ох.
Решение. Из рисунка 10 видно, что искомая площадь может быть представлена как сумма площадей: 
где BA и MN—перпендикуляры, опущенные из точек В и Al на ось Ох.
Определим координаты точек В, С, М, Р. Для этого решим следующие системы уравнений:
Решая систему (I) уравнений, найдем координаты точек В и M : В (I, 2), M {— I, 2).
Решая систему (2) уравнений, найдем координаты точки С : С (3, К».
Решая систему (3) уравнений, найдем координаты точки P : Р(— 2, 5).
Найдем теперь значения промежуточных площадей:
Отсюда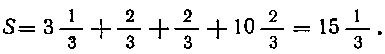
449. Найти площадь фигуры, ограниченной линиями:
450. Найти площадь фигуры, ограниченной линиями:
451. Найти площадь фигуры, ограниченной параболами:
452. Найти площадь фигуры, ограниченной линиями:
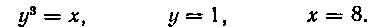
453. Найти площадь фигуры, ограниченной линиями:
454. Найти площадь «Ьигуоы. огоаниченной линиями:
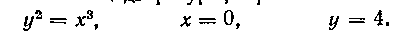
455. Найти площадь круга:
456. Найти площадь эллипса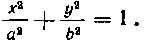
457. Найти площадь, заключенную между кривыми
458. Найти площадь фигуры, ограниченной гипоци-лоидой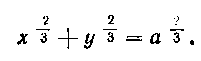
459. Найти площадь фигуры, ограниченной гиперболой
И прямой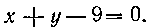
460. Вычислить площадь фигуры, заключенной между параболой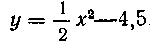
, осями координат и прямой х=3,5.
461. Найти площадь фигуры, заключенной между кривыми:
462. Найти площадь частей эллипса
отсеченных гиперболой
463. Найти площадь фигуры, ограниченной кривой
464. Найти площадь фигуры, заключенной между кривыми
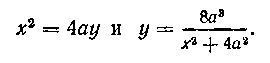
2. Кривые заданы параметрическими уравнениями. Если кривая, ограничивающая площадь плоской фигуры, задана параметрическими уравнениями:
где функции
Непрерывны вместе со своими про
изводными на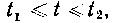
То для вычисления площади
плоской фигуры следует в определенном интеграле произвести замену переменной: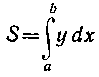
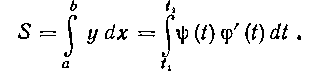
465. Вычислить площадь, ограниченную эллипсом!
Решение. Эллипс расположен симметрично относительно обеих осей (рис. Последовательно, можно вычислить сначала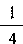
• часть площади данной фигуры. Вычислим площадь той части плоской фигуры, которая расположена в первом квадранте:
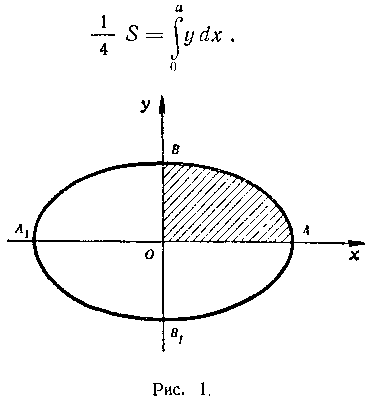
Найдем пределы интегрирования для переменной t из условий:
Имеем:
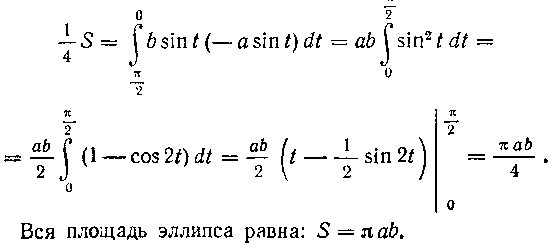
466. Найти площадь фигуры, ограниченной астроидой:
PsP ш е н и е. Искомая площадь изображена на рисунке 12. Вычислим сначала площадь тсй части плоской фигуры, которая расположена в первом квадранте, это будет
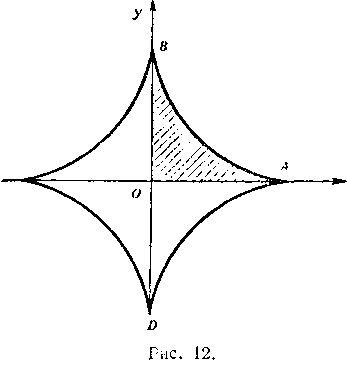
Рис. 12.
часть всей искомой площади. Найдем пределы интегрирования для переменной / из условий:
Следовательно,
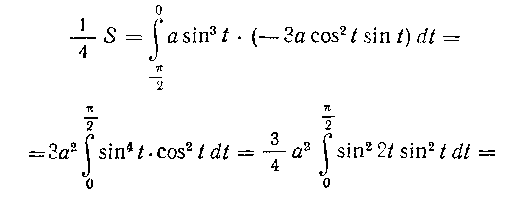
467. Вычислить площадь, ограниченную одной аркой циклоиды: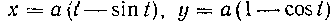
И осью Ох.
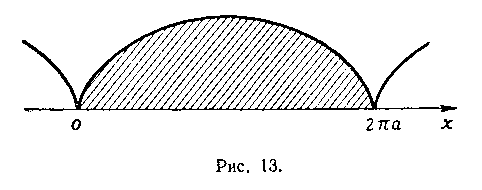
Решение. Из рисунка 13 видно, что при изменении параметра t от 0 до 2л точка (ху у) обегает всю арку циклоиды, причем х изменяется в промежутках от 0 до 2т. Следовательно,
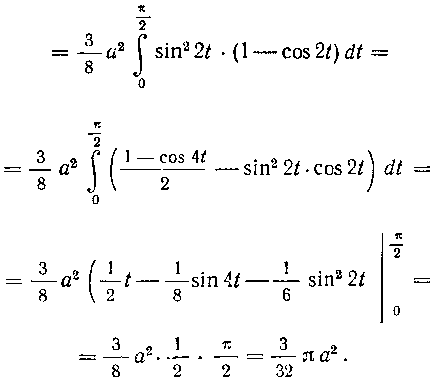
Вся площадь, ограниченная астроидой, равна:
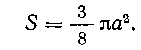
о
468. Вычислить площадь четверти круга: x = 2cos t, y = 2sint.
469. Найти площадь, ограниченную эволютой эллипса:
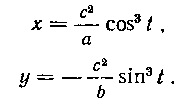
(.Эволютой кривой называется геометрическое место её центров кривизны. Эволютой эллипса является деформированная астроида.)
470. Найти площадь, ограниченную кардиоидой:
х = a(2cost — cos 21), у = a (2sin/— sin 2/).
3. Кривые заданы в полярной системе координат. Из
теоретического курса известно, что площадь S1 ограниченная неподвижным полярным радиусом г0, подвижным полярным радиусом г и кривой г — /(ф), может быть вычислена по следующей формуле:
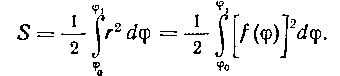
<Р> Ч, г
S = - j J/-2 Лр = J - j /(<р)]2<*Ф.
90
471. Вычислить площадь, ограниченную первым витком спирали Архимеда г — а<р (рис. 14).
Решение. Найдем пределы интегрирования. Первый виток спирали образуется при изменении параметра t от О до 2зх. Следовательно,
D3 Д
472. Найти площадь, ограниченную одним лепестком кривой г = a sin 2<р.
Решение. Пределы интегрирования для <р найдем из условий:
Отсюда
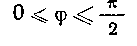
и, следовательно,
473. Вычислить площадь, ограниченную кривой г = = a cos ф.
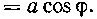
Решение. Данная кривая—окружность радиуса у,
проходящая через полюс, расположенная симметрично относительно полярной оси. Эго легко увидеть, если перейти к декартовым координатам. (Проделайте это самостоя-
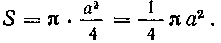
а2 I
тельно.) Тогда S = я - — = —я;а2.
Можно было найти искомую площадь, используя полярное уравнение данной кривой. Пределы для q> найдут* ся из условия cos ф> 0, следовательно,
1C
T
S = J a® cos2 ф dq> =
--< ф < —.
Таким образом, имеем:
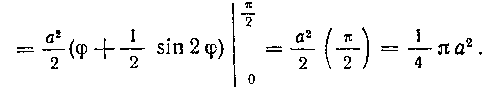
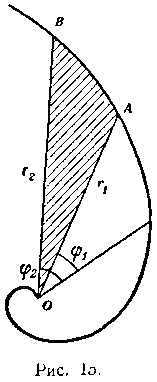
474. Вычислить площадь OAB (см. рис. 15), ограниченную полярными радиусамиг, = OA и r2 = OB и дугой логарифмической спирали
Решение. Будем считать, что полярному радиусу г, соответствует полярный угол фг, а полярному радиусу г2 соответствует полярный угол ф2. Тогда
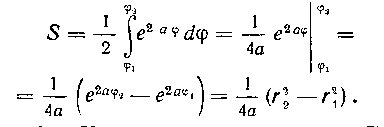
475. Найти площадь петли листа Декарта: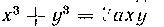
Решение. Перейдем к полярным координатам с помощью известных соотношений:
Уравнение данной кривой в полярных координатах примет вид:
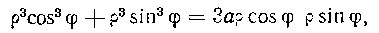
откуда
На получим
откуда
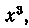
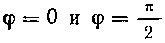, в этом промежутке изменения полярного
углаф кривая опишет петлю. При
Или
знаменатель стремится к нулю и, следовательно, р —» оо. Это значит, что существует асипмтота данной кривой. Найдем ее, пользуясь исходным уравнением кривой в лекап-товых координатах. Разделив обе части равенства
Из полученного уравнения кривой видно, что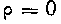
При
HO
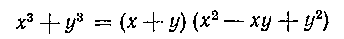
и, следовательно, таким образом,
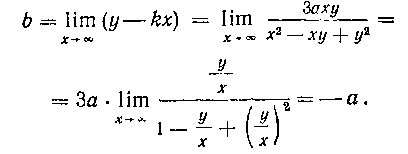
Уравнение асимптоты:
Подставляя вместо k и b найденные значения, получим искомое уравнение асимптоты данной кривой:
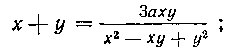
Для построения данной кривой совместим полюс с началом декартовых координат и будем считать положительное направление оси Ox совпадающим с направлением полярной оси. Составим таблицу значений
Соединяя теперь плавной кривой полученные точки, получим петлю данной кривой (рис. 16).
Найдем площадь, ограниченную петлей листа Декарта. Из геометрических соображений видно, что полярный угол <р
изменяется от 0 до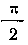
.Tаким образом, находим:
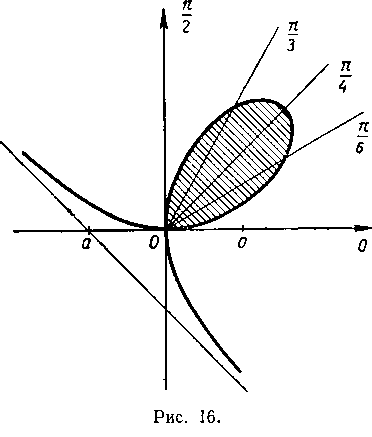
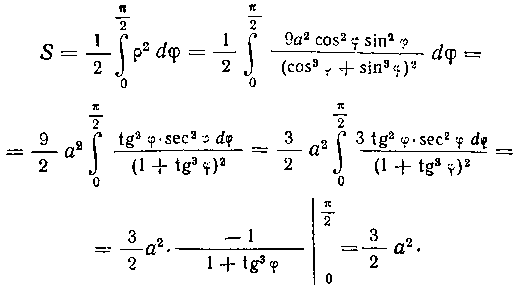
476. Вычислить площадь круга
477. Найти площадь, ограниченную петлей лемнискаты>
Построив предварительно данную кривую.
478. Найти площадь, ограниченную кривой:
P = a cos 4<р.
479. Найти площадь, ограниченную одним лепестком кривой:
P = a cos 2ф.
480. Найти площадь фигуры, ограниченной вторым витком спирали Архимеда р = аф и отрезком полярной оси, соединяющим концы первого и второго витков (см. рис. 14).
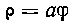
481. Найти площадь, ограниченную улиткой Паскаля:
P = 2а (2 cos ф).
482. Вычислить площадь, ограниченную кардиоидой:
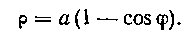
P = а (I — cos ф).
| < Предыдущая | Следующая > |
|---|
