4.4. Объемы и поверхности тел вращения

I. Объемы тел вращения. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п°п° 197, 198* Разберите подробно примеры, приведенные в п° 198.

508. Вычислить объем тела, образуемого вращением эллипса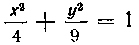Вокруг оси Ох.

Решение. При вращении эллипса вокруг оси Ox образуется тело, называемое эллипсоидом вращении. Как известно, объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху кривой у = f{x), ординатами х = а, х = Ь и осью Ох, вычисляется по формуле:

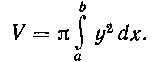
Из уравнения эллипса видно, что большая его полуось равна 2, следовательно,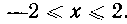. Разрешив уравнение

эллипса относительно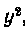, получим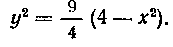Объем

эллипсоида вращения равен:

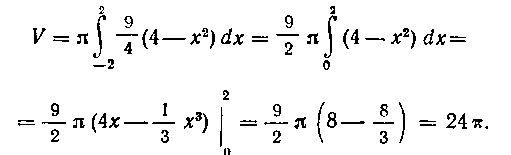
509. Найти объем тора, образованного вращением круга

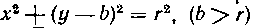Вокруг оси Ox (рис. 18). Решение. Искомый объем тора равен разности объемов, полученных от вращения верхнего и нижнего полукругов. Так как для верхнего полукруга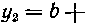

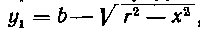, а для нижнего, то

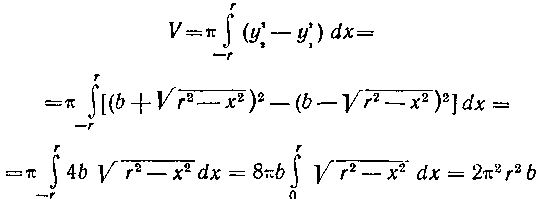
(см. задачу 388).

Б10. Вычислить объем прямого конуса, высота которого h и радиус основания г, рассматривая конус как тело вращения прямоугольного треугольника около одного из катетов.

Решение. Выберем систему координат так, чтобы ось Ox совпала с высотой h (рис. 19), а вершину конуса

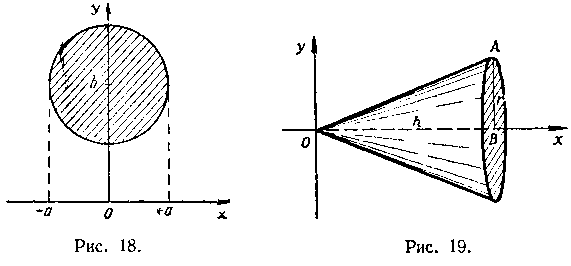
примем за начало координат. Тогда уравнение прямой OA

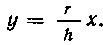
Следовательно, объем конуса

запишется так: будет равен:

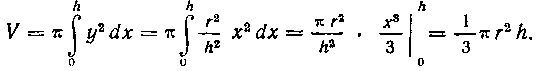
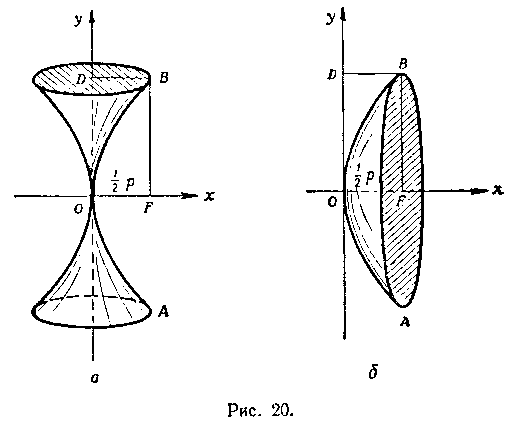
511. Вычислить объемы тел, образованных вращением около осей Ox и Oy сегмента AOB параболы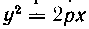, от

секаемого хордой AFB, проходящей через фокус параболы перпендикулярно к оси Ox (рис. 20, а, б).

Решение I. Вычислим объем тела, получаемого при вращении сегмента AOB вокруг оси Ох, пользуясь формулой: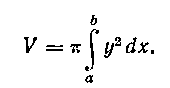

Найдем пределы интегрирования. Прямая AB параллельна оси Oy. Ее уравнение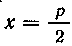. Для того чтобы

найти точки пересечения этой прямой с параболой, решим совместно систему уравнений:

мя я AB проходит через фокус параболы, то координаты точки F будут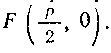Следовательно,

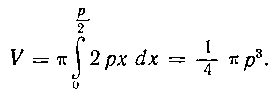
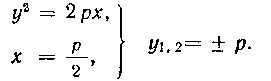
Получим точки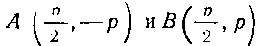. Так Kaw пря

2. Вычислим объем тела, получаемого при вращении сегмента AOB вокруг оси Oy. Учитывая симметрию сегмента относительно оси Oxi найдем сначала половину искомого объема. Она равна разности объемов тел, получаемых от вращения вокруг оси Oy прямоугольника OFBD и криволинейного тоеугольника OBD. Так как объем цилиндра равен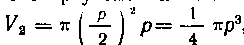, а объем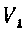Тела, полученного от вращения криволинейного треугольника OBD вокруг оси Oy, будет:

512. Фигура, ограниченная гиперболо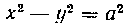йИ

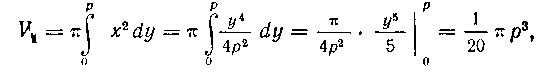
то половина искомого объема равна:

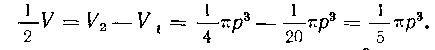
Следовательно, весь искомый объем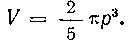

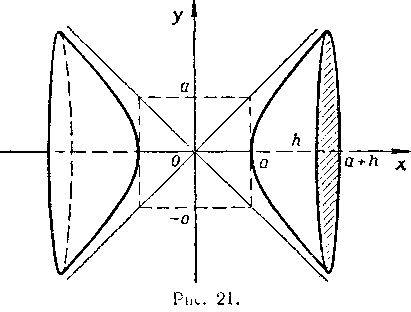
прямыми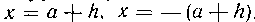, вращается вокруг оси

Ох. Найти объем тела вращения.

Решение. В результате вращения данной фигуры вокруг оси Ox образуются два тела вращения, имеющие равные объемы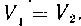Тогда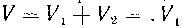

Найдем объем V1 тела (рис. 21), сбразованного вращением площади, ограниченной правей ветвью гиперболы 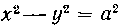И прямей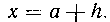Пределы интегрирова

ния найдем из геометрических соображений: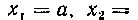

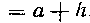. Таким образом,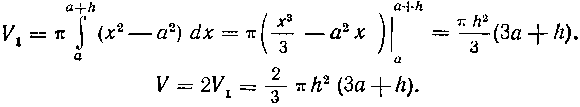

513. Вычислить объем тела, образованного вращением вокруг оси Ox одной полуволны синусоиды у = sin х.

514. Найти объем конуса, производимого вращением вокруг оси Ox части прямой _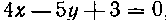, содержащейся между осями координат.

515. Криволинейная трапеция, ограниченная срерху параболой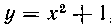,с боков—ординатами х = — I и х—\, снизу — осью Ох, вращается вокруг оси Ох. Найти объем полученного тела вращения.

516. Вычислить объем тела, образованного вращением вокруг оси Ox площади, ограниченной цепной линией

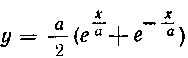, ординатами X = — а, х = а и осью Ох.

517. Прямой параболический сегмент, основание которого а, а высота R, вращается вокруг основания. Определить объем полученного тела вращения.

518. Найти объем цирка, осевое сечение которого — парабола. Высота цирка 30 м. Диаметр основания 50 м.

519. Найти объем тела, образованного вращением кривой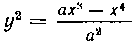Вокруг оси абсцисс.

520. Вычислить объем тела, полученного вращением

астроиды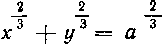Вокруг оси Oy.

521. На кривой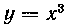Взяты две точки А и В, абсциссы которых соответственно а = I и Ь = 2. Найти объем тела, полученного вращением криволинейной трапеции аАВЬ вокруг оси Ох.

522. Найти объем тела, производимого вращением площади, ограниченной дугой циклоиды,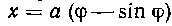

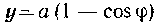И осью Ox вокруг ее основания.

523. Вычислить объем тела, образованного вращением вокруг оси ординат дуги OM циклоиды,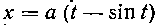

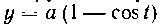, ограниченной точками О (0, 0) и M (та*, 2а).

524. Найти объем тела, ограниченного поверхностью, полученной при вращении линии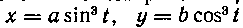

вокруг оси абсцисс.

2. Площадь поверхности тела вращения. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 205. В теоретическом курсе показано, что площадь поверхности тела вращения определяется по формуле:

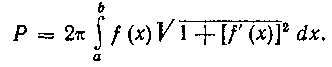
52$. Определить площадь поверхности параболоида, образованного вращением дуги параболы у2 = 2х вокруг оси Ox от х = 0 до х = 2.

Решение. В нашем случае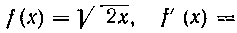 . Поэтому

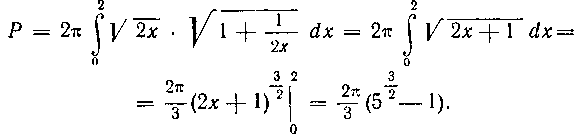
526. Найти площадь поверхности шара радиуса R. Решение. Поместим начало координат в центре шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружности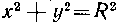Вокруг оси Ох. Тогда площадь поверхности шара найдется по формуле:

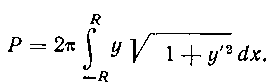
T ак как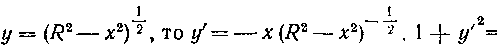

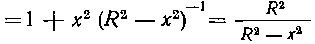И, следовательно,

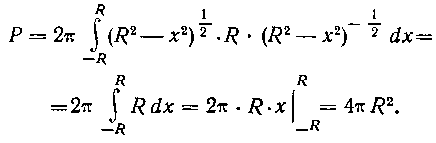
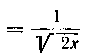
527. Найти площадь поверхности эллипсоида, образованного вращением эллипсаВокруг оси Ох.

Решение. Из уравнения эллипса имеем: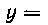

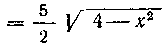. Найдем производную: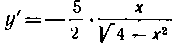

Тогда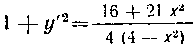. Так как полуось эллипса

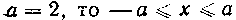И, следовательно,

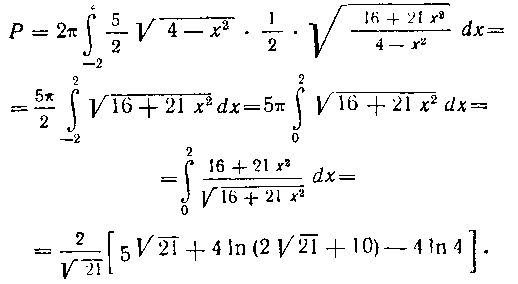
Если кривая задана параметрически, то, заменяя переменную под знаком определенного интеграла, получим для площади поверхности следующую формулу:

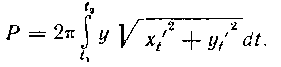
528 Вычислить площадь поверхности, сбразованной вращением одной арки циклоиды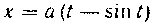

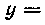
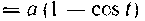Вокруг оси Ox (см. рис. 13).

Решение. Найдем:

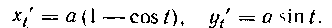
Тогда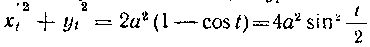. Искомая по

верхность равна:

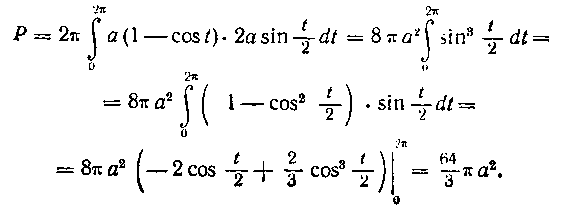
Решение. Построим данную кривую. Найдем точки пересечения ее с осями координат.

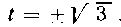
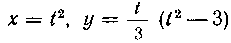
нием петли кривой х = /2, у

(/2— 3) вокруг оси Ох.

При у — 0 находим t = 0 и t = ±}/ 3 . Следовательно, X1 = 0 и X2 -= 3* т. е. кривая пересекает ось Ox в двух точках О (0, 0) и А (3, 0).

При х = 0 находим / = 0, следовательно, у = 0. Мы получили ту же точку О (0, 0).

При люб dx вещественных значениях параметра / будут вещественны х и у Так как х — четная функция параметра /, у — нечетная функция параметра /, то график расположен симметрично относительно оси Ох.

Исследуем данную функцию на экстремум. Находим производную:

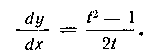
dy = /2-dx 21

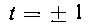
Легко видеть, что у = 0 при / = + I и, следовательно^

У

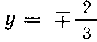
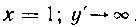
у — + —; когда X= I; у'-* оо, когда / —> 0, следовательно,

когда х -> 0, то и у 0. Это значит, что в начале координат касательная к данной кривой вертикальна. В точке

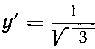
А (3; 0) будет у' = - J=, это значит, что касательная У з

к данной кривой в этой точке образует с положительным направлением оси Ox угол в 30°.

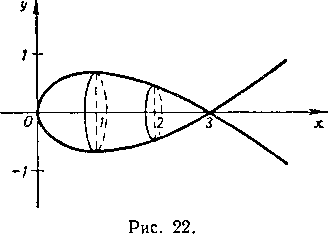
Полученных данных достаточно для построения графика данной функции (рис. 22).

Найдем площадь данной поверхности. Имеем: х' = 21, y' = f - I; х'% -(-y'z = (I +12 )а.

З о

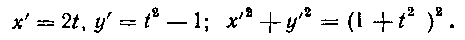
Таким образом,

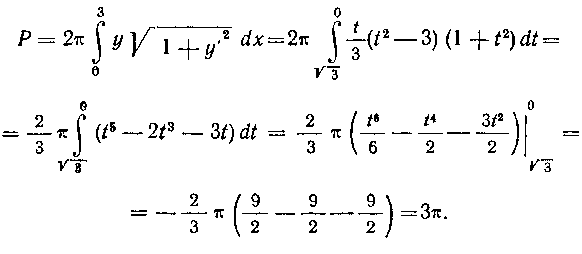
Р=2* Jyj/T^T |±(<*_3)(1+/«)Л =

0 KT

IrF ^ з

3 Ik 2 2 2 /

530. Найти площадь поверхности, образованной вращением вокруг оси Ox дуги синусоиды у = sin х от точки X = 0 до точки X = It.

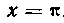
531. Вычислить площадь поверхности конуса с высотой h и радиусом г.

532. Вычислить площадь поверхности, образованной

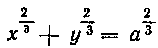
2_ 2_ 2_

вращением астроиды х3 -)- у* — а3 вокруг оси Ох.

533. Вычислить площадь поверхности, образованной цращением петли кривой 18 уг — х (6 — х)г вокруг оси Ох.

534. Найти поверхность тора, производимого вращением круга X2 - j - (у—З)2 = 4 вокруг оси Ох.

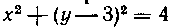
535. Вычислить площадь поверхности, образованной вращением окружности X = a cost, y = asint вокруг оси Ох.

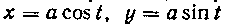
536. Вычислить площадь поверхности, образованной вращением петли кривой х = 9t2, у = St — 9t3 вокруг оси Ох.

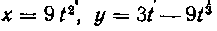
537. Найти площадь поверхности, образованной вращением дуги кривой х = е*sint, у = el cost вокруг оси Ox

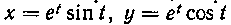
от t = 0 до t = —.

2

538. Показать, что поверхность, производимая вращением дуги циклоиды х = a (q> —sin ф), у = а (I — cos ф) вокруг оси Oy, равна 16 и2 о2.

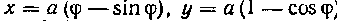
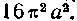
539. Найти поверхность, полученную вращением кардиоиды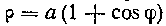Вокруг полярной оси.

540. Найти площадь поверхности, образованной вращением лемнискаты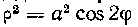Вокруг полярной оси.

Дополнительные задачи к главе IV

Площади плоских фигур

541. Найтивсю площадь области, ограниченной кривой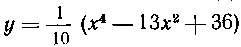И осью Ох.

542. Найти площадь области, ограниченной кривой

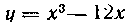И осью Ох.

543. Найти часть площади области, расположенной в первом квадранте и ограниченной кривой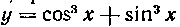

л осями координат.

544. Найти площадь области, содержащейся внутри

петли: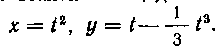

545. Найти площадь области, ограниченной одной петлей кривой: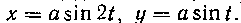

546. Найти площадь области, содержащейся внутри петли: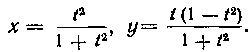

547. Найти площадь области, ограниченной кривой

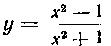И осью Ох.

548. Найти площадь области, ограниченной кривой

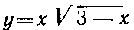И осью Ох.

549. Найти площадь области, ограниченной осью Oxr

прямой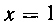И кривой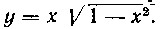

550. Найти площадь области, ограниченной кривыми.

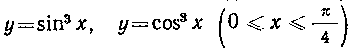И осью Oy.

Вычисление длины дуги

551. Найти длину дуги кривой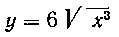От точки А(0: до точки В (I: 6).

552. Найти длину дуги CD кривой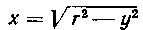, где

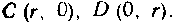Дать геометрическую иллюстрацию.

553. Найти длину дуги OA кривой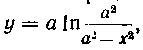Где

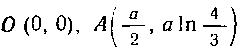
554. Найти длину дуги AB кривой у = еху где А (0; I), В (I; 2)

555. Нгйти длину дуги AB кривой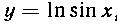, где

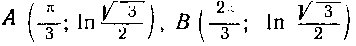
556. Нгйти длину дуги кривой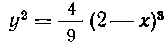, отсеченной прямей X = — I.

557. Нгйти длину дуги кривой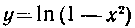От

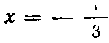До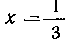

Объем тела вращения

558. Нгйти объем тела, полученного вращением вокруг юси Ox п/ощоди, сграниченной крквой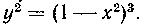

559. Нййти объем тела, полученного от вращения рокруг сси Ox площади, ограниченной кривой

560. Найти объем тела, образованного вращением вокруг оси Oy площади, ограниченной кривой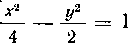

ц прямыми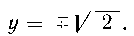

561. Найти объем тела, образованного вращением вокруг оси Oy площади, ограниченней эллипсом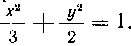

562. Нгйти объем тела, полученного вращением вокруг оси Oy плещади, ограниченной кривой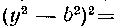

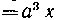И отрезком оси Oy.

563. Найти объем тела, полученного вращением вокруг оси Ox площади, ограниченной кривой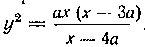

564. Круг радиуса 2 с центром в точке (7; 0) вращается вокруг оси Oy. Определить объем полученного тела вращения.

565. Нлйти объем тела, полученного вращением вокруг оси Ox площади, расположенной в первом квадранте и

ограниченной кривой(эволюта

эллипса).

Площадь поверхности вращения

566. Найти площадь поверхности, образованной вращением дуги кривой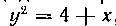, отсеченной прямой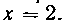

567. Найти площадь поверхности шаоовой чаши, полученной при вращении круга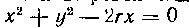Вокруг оси Ox в пределах от 0 до h.

568. Найти площадь поверхности катеноида, образованного вращением вокруг оси абсцисс цепной линии

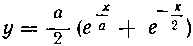От точки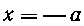До точки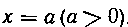

569. Найти площадь поверхности эллипсоида, образованного вращением эллипса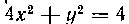Вокруг оси Oy.

570. Найти площадь поверхности, образованной вращением вокруг оси Ox петли кривой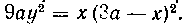

571. Найти площадь поверхности, образованной вращением вокруг оси Ox кривой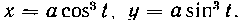

572. Найти площадь поверхности, образованной вращением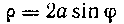Вокруг полярной оси.

ПРИЛОЖЕНИЯ К ВОПРОСАМ ФИЗИКИ

< Предыдущая		Следующая >