4.3. Объем тела произвольной формы
Предварительно изучите по учебнику Г. М. Фихтен-гольца главу XII, п°п° 197, 198.
В теоретическом курсе показано, что объем тела, содержащегося между плоскостями х = а и х = Ь, выражается формулой:
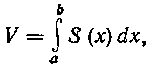
где S (х) — площадь сечения тела плоскостью, перпендикулярной к оси абсцисс в точке х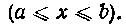
503. Вычислить объем шарового слоя, вырезанного из шара х2 + у2 -)- Z2 = 9 плоскостями х — I и х = 2.
Решение. Плоскость, перпендикулярная к оси абсцисс в точке Xt пересечет шар по окружности радиуса г = |/ 9 — лг. Площадь сечения S (х) = пг2 = я (9 — х2) и, следовательно,
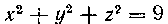
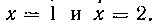
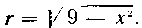
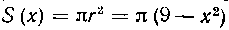
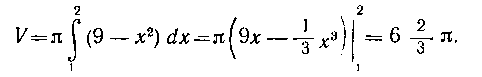
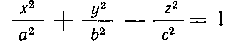
стями Z = о И 2=1.
Решение. Обозначим через Q (z) площадь сечения тела плоскостью, перпендикулярной к оси Oz. В сечении получим эллипс:
у2 </2 у2
Л. - L JL_ = I C2 Г 62 ' C2
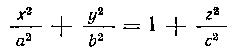
~2 «.2 +
или
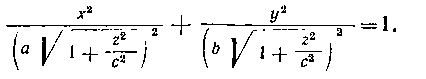
Так как полуоси этого эллипса равны а i/i+
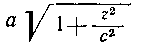
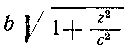
6 у i_|_ , а, как известно, площадь эллипса равна nab,
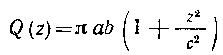
( Z2 \
то, следовательно, Q (г) =я ab / I -\--- I. Таким образом,
I I
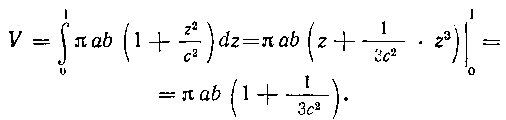
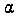
V = jnab 11 -?j^dz=nab • Z3J =
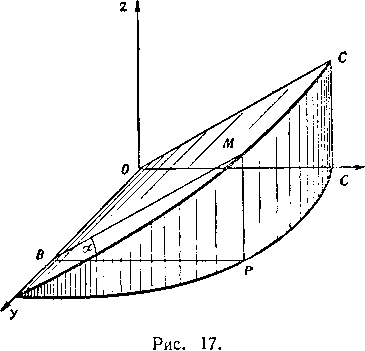
505. От прямого кругового цилиндра радиуса а отсечен клин плоскостью, проходящей через диаметр основания и наклоненной к основанию под углом а (рис. 17). Найти объем клина.
Решение. Выберем систему координат так, чтобы ось цилиндра совпала с аппликатой (см. рис. 17). Разобьем Клин на слои плоскссгями, перпендикулярными к оси Ох.
504. Вычислить объем тела, ограниченного однополо-
стным гиперболоидом--1- —---= I и плоско-
а2 Ь2 с2
Тогда в сечении клина плоскостью, отстоящей на расстояние х от начала координат, получим прямоугольный треугогьник MPBi укоторого катет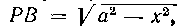 катет
катет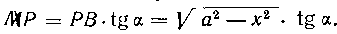 Отсюда
Отсюда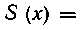
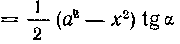 И
И 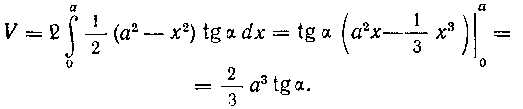
508. Вычислить путем интегрирования объем правильной четырехугольной пирамиды со стороной основания а и высотой H.
507. Определить объем тела, отсеченного от круглого цилиндра плоскостью, проходящей через диамэтр основания. Радиус основания равен Rf высота тела равна Я.
| < Предыдущая | Следующая > |
|---|