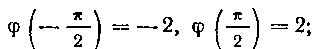3.3. Замена переменной. Интегрирование но частям
I. Замена переменной в определенном интеграле.
Предварительно изучите по учебнику Г. М. Фихтенголь-ца главу XI, п° 186. Разберите примеры, решенные в этом пункте. Обратите особое внимание на выполнимость условий, при которых становится возможной замена переменной.
В теоретическом курсе доказывается, что определен-
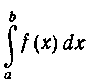
рый интеграл при выполнении ряда условий мо-
экет быть заменен другим определенным интегралом
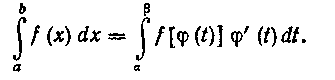
Замечание. При вычислении определенного интеграла с помощью замены переменной нет необходимости затем возпращаться к стар эй переменной (как мы это делали при вычислении неопределенного интеграла).
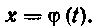
При этом используется замена переменной
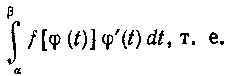
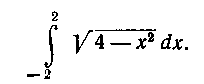
Решение. Введем новую переменную t, положив 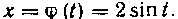 Покажем, что функция
Покажем, что функция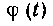 Удовлетворяет всем условиям теоремы о замене переменной в определенном интеграле. В самом деле,
Удовлетворяет всем условиям теоремы о замене переменной в определенном интеграле. В самом деле,
I) функция, w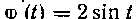 ______ определена и непрерывна
______ определена и непрерывна
для всех значений t и, в частности, на некотором промежутке
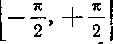
, и ее значения не выходят за пределы промежутка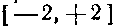 , когда t изменяется в
, когда t изменяется в
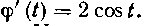
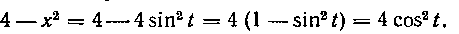
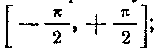
3) существует в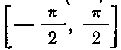 Непрерывная производная
Непрерывная производная
Итак, указанная замена переменной законна. Тогда
для
Так как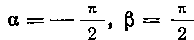 -, то, заменяя переменную в
-, то, заменяя переменную в
определенном интеграле и учитывая четность подынтегральной функции, получим:
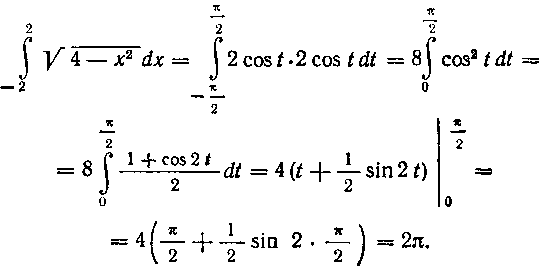
Указание. Для отыскания пределов интегрирования новой переменной t используйте равенство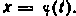 Нижний предел а найдется, если вместо х подставить значение нижнего (старого) предела:
Нижний предел а найдется, если вместо х подставить значение нижнего (старого) предела:
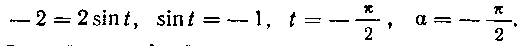
Верхний предел р найдется, если вместо х подставить значение верхнего (старого) предела:
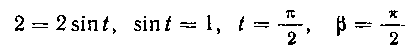
389. Вычислить интеграл:

Решение. Введем новую переменную t, связанную со старой переменной х соотношением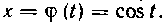 Покажем, что такая замена переменной законна.
Покажем, что такая замена переменной законна.
Действительно: I) функция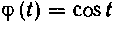 Определена и
Определена и
непрерывна на отрезке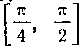 (так как она определена
(так как она определена
и непрерывна на всей числовой поямой). и ее значения не выходят за пределы промежутка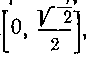 Когда t изменя
Когда t изменя
ется в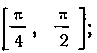
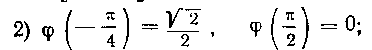
3) существует в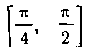 Непрерывная производная
Непрерывная производная
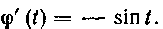
Итак, вводим новую переменную t, полагая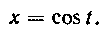 Тогда
Тогда
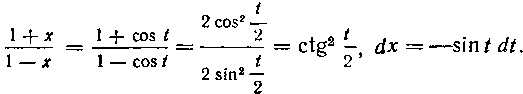
Так как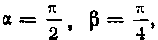 То, заменяя переменную в опре-
То, заменяя переменную в опре-
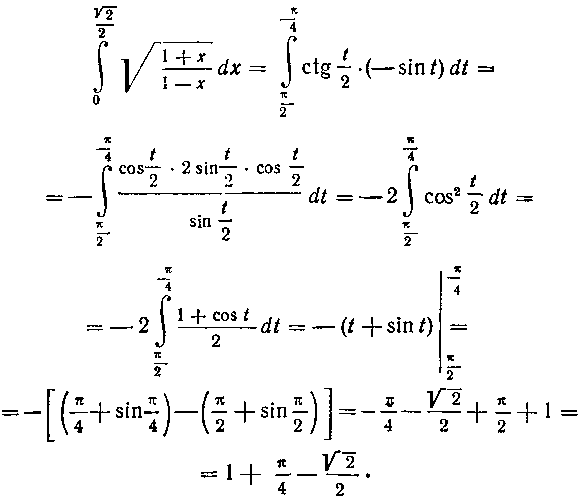
390. Вычислить интеграл: ;.
Решение. Введем новую переменную t, положив х = te. (Почему возможна такая замена?) Тогда dx = = 6 tbdt. Найдем пределы интегрирования для новой переменной t:
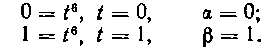
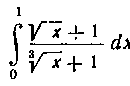
Заменяя переменную в определенном интеграле, получим
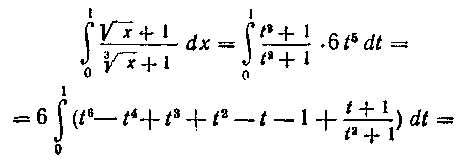
Применяя соответствующую замену переменной, вычислить интегралы:
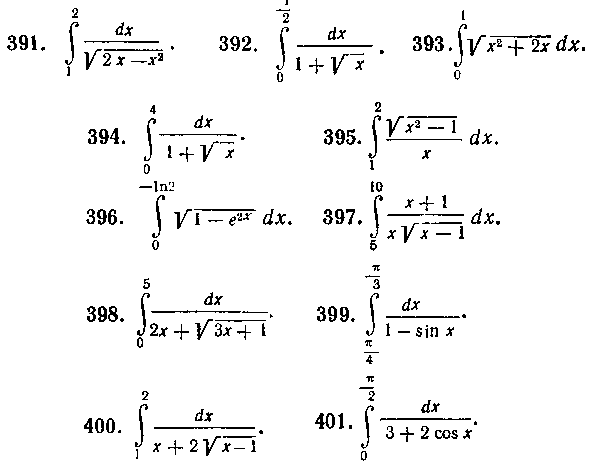
2. Интегрирование по частям в определенном интеграле.
Рассмотрите внимательно решение примеров, помещенных в п° 187. Обратите особое внимание на выполнение необходимых условий, при которых операция интегрирования по частям будет законна.
402. Вычислить интеграл:
Решение. Обозначим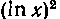 Через и, а
Через и, а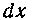 Через
Через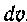 ,
,

120
Эта операция является законной, так как в промежутке [I, 2] функции и и V являются непрерывными функциями и имеют непрерывные производные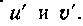
В теоретическом курсе было показано, что при выполнении этих условий
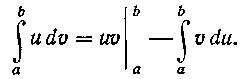
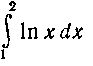
Следовательно,
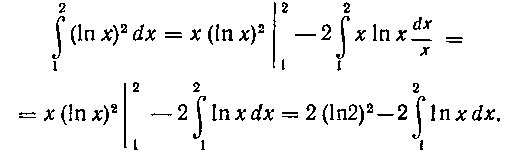
Интеграл снова берем по частям, полагая

(Мы пропускаем доказательство законности данной операции, так как оно аналогично доказательству, приведенному ранее.)
Получим:
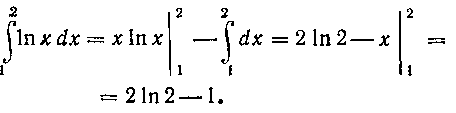
Окончательно получим: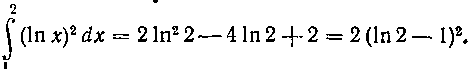
403. Вычислить интеграл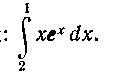
Решение. Обозначим х через и и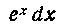 Через dv,
Через dv,

Легко показать, что данная операция является законной: функции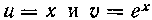 —функции непрерывные и име
—функции непрерывные и име
ют в каждой точке промежутка [О, I] непрерывные производные. Следовательно,
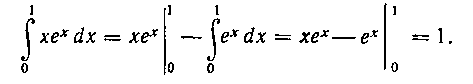
Используя метод интегрирования по частям, вычислить следующие интегралы:
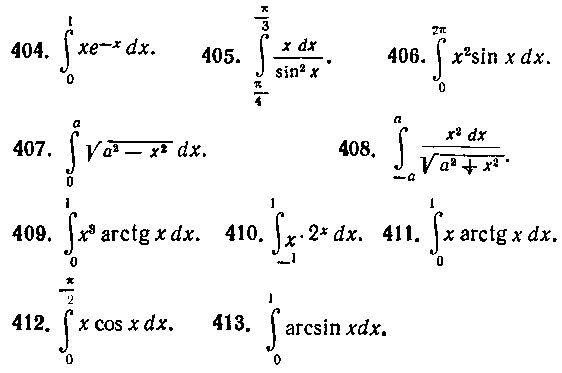
Метод интегрировайия по частям в определенном интеграле часто используется для получения удобных рекуррентных формул, позволяющих сводить данный интеграл к интегралу такого же типа, но более простому.
414. Вычислить интеграл:
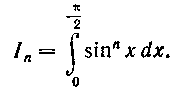
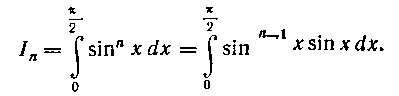
Применяя метод интегрирования пр частям* положим:
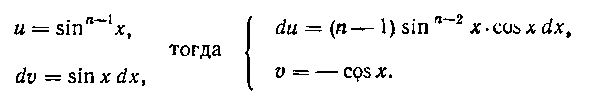
Итак,
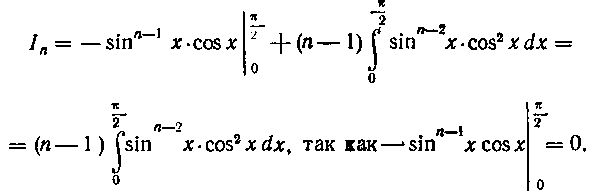
Выполняя простые тригонометрические преобразования^ получим:
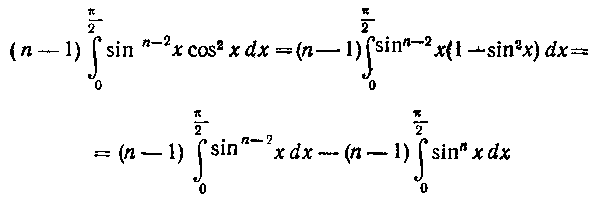
или
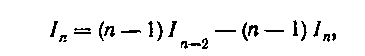
где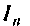 Обозначает
Обозначает
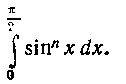
Мы получили уравнение относительно /„, решая которое получим рекуррентную формулу для вычисления In:
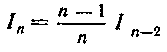
(Сравни с формулой (19) на стр. 86). Применяя аналогичные преобразования, получим:
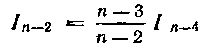
или
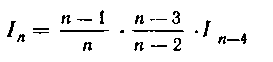 И т. д.
И т. д.
Продолжая указанный процесс, мы дойдем или до значения /0, или до значения I1 в зависимости от того, будет ли п четным или нечетным числом.
Рассмотрим два случая:
I)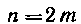 («—четное число). В этом случае
(«—четное число). В этом случае
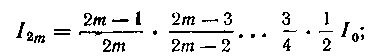
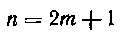
2) (п — нечетное число). В этом случае
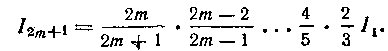
Ho так как

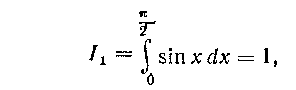
то
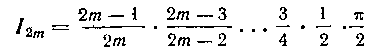
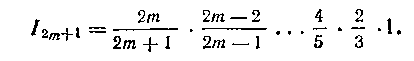
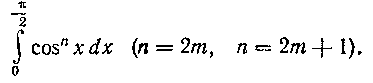
416. Составить рекуррентную формулу для вычисления
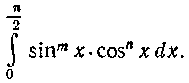
417. Доказать равенство:
интеграла Провести исследование.
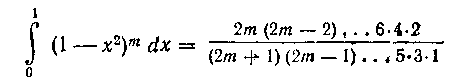
(т — целое положительное число).
418. Вычислить, используя результат примера 414:
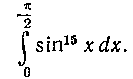
419. Вычислить, используя результат примера 415:
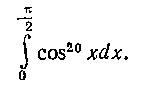
| < Предыдущая | Следующая > |
|---|