3.4. Приближенное интегрирование

Предварительно изучите по учебнику Г. М. Фихтен-гольца главу XI, п° 189 —190. Разберите примеры, приведенные в п° 192.

420. Вычислить приближенно:

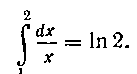
Решение. Функция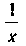Задана на сегменте 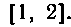Разобьем сегмент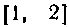На 10 равных частей. Тогда

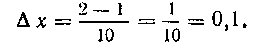
Используем для вычисления одну из формул приближенного интегрирования.

1. Применим первую формулу прямоугольников (значение интеграла получается с избытком):

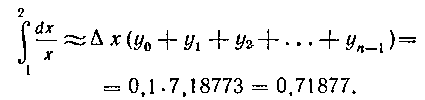
2. Применим вторую формулу прямоугольников (значение интеграла получается с недостатком):

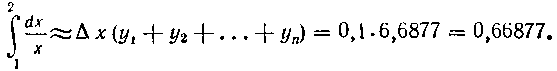
3. Применим формулу трапеций:

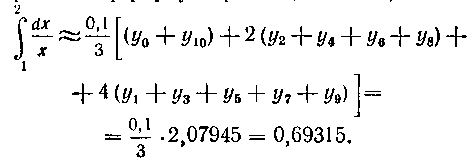
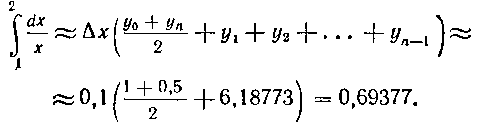
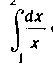
4. Применим формулу парабол (Симпсона):

Более точное вычисление значения In 2 дает число

0,6931472.

Таким образом, формула Симпсона дает совпадение до пяти значащих цифр. Наименее точный результат дает формула прямоугольников (один верный знак).

Замечание. Совершенно очевидно, что точность вычисления увеличивается с возрастанием числа точек деления. ,Всегда можно подобрать достаточное число точек деления так, чтобы производить вычиспения с любой наперед заданной степенью точности.

Для определения числа точек деления, необходимых для вычисления интеграла с заданной степенью точности, сложно воспользовался формулами оценки погрешности, приведенными в п° 191 учебника Г. М. Фихтенгольца.

421. Применяя формулу Симпсона, вычислить значение я

из соотношения

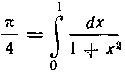
(при вычислении примите

п = 10).

422. Применяя формулу Симпсона, вычислить приближенное значение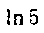Из соотношения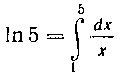(при вы-

числении примите п = 10).

423. По следующей таблице значений х и f(x)

ТТТХ^ТТ^ТТТТТХ ГТ^Л/ГТТ'Г о и _ 1П\

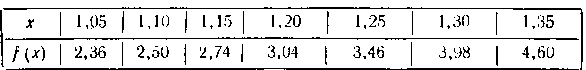
вычислить интегралпользуясь формулой

Симпсона,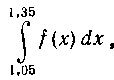

Дополнительные задачи к главе VII

Пользуясь ойределением определенного интеграла, вычислить интегралы:

426. Найти среднее значение функции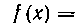

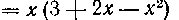На отрезке [I, 2].

427. Найтисреднее значение функции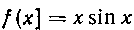 на отрезке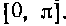

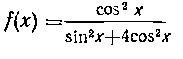
428. Найти среднее значение функции

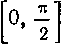
па uipcorvt •

Следующие определенные интегралы вычислите с помощью замены переменной.

Указание. Воспользуйтесь подстановкой х = 3 tg t.

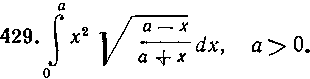
Указание. Воспользуйтесь подстановкой х = a cos t

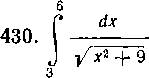
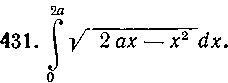
Указание. Воспользуйтесь подстановкой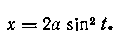

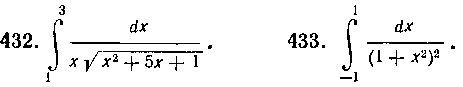
I —I

Найти производные следующих функций:

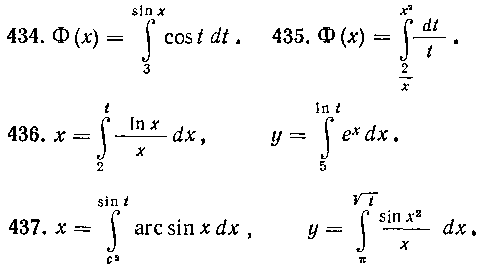
Найти экстремум следующих функций;

х_£_

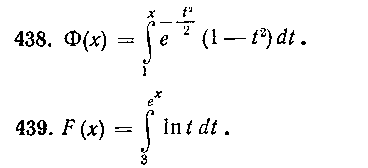
2 2

438. Ф(ж) = Je 2 (I — t2)dt.

439. F(x) = J Intdt.

3

Применяя формулу интегрирования по частям, вычис

лить интегралы:

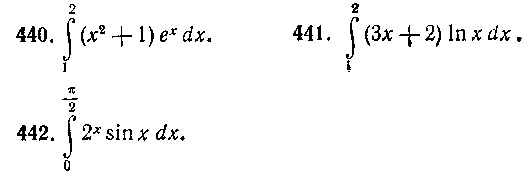
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА К ГЕОМЕТРИИ

< Предыдущая		Следующая >