3.1. Вычисление непосредственным суммированием
I. Вычисление с помощью интегральных сумм. Предварительно изучите по учебнику Г М. Фихтенгольца главу XI, п° 176, 177, 180, 184. Обратите особое внимание на примеры, решенные в п° 184.
Способ вычисления определенных интегралов методом суммирования основан на понятии «интегральных сумм», подробно изложенном в п°п° 176, 184.
321. Вычислить интеграл:

Решение. В теоретическом курсе (п° 176) доказывается, что
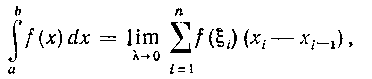
где f(x) — непрерывная на сегменте Функция, Ii —
Функция, Ii —
точка, произвольно выбранная внутри частичного сегмента  , а X—максимальная из длин частичных сегментов. Из определения определенного интеграла следует, что значение
, а X—максимальная из длин частичных сегментов. Из определения определенного интеграла следует, что значение
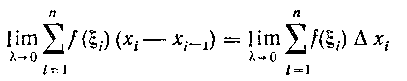
не зависит ни от способа разбиения сегмента На
На
частичные сегменты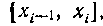 Ле от выбора точки
Ле от выбора точки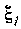
внутри каждого из частичных сегментов. Руководствуясь этим, разобьем сегмент [О, I] на п равных частей. Точками деления сегмента будут:
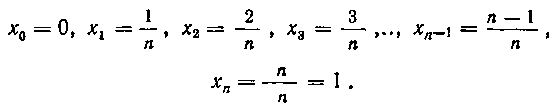 I
I
Получим п частичных сегментов:
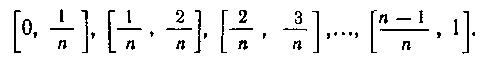
Длина каждого из частичных сегментов равна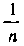 . Заметим, что
. Заметим, что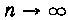 При
При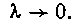
Выберем внутри каждого частичного сегмента наиболее удобное для вычисления положение точек Ii. Пусть это будут самые правые точки каждого частичного сегмента:
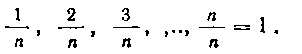
Вычислим значение функции /(Ii) в этих точках:

Составим интегральную сумму:

Вычислим предел интегральной суммы при , ,:
, ,:
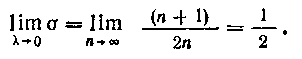
Таким образом, 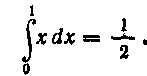
Покажем, что и при другом выборе точек Результат будет тот же. В самом деле, пусть в качестве точек
Результат будет тот же. В самом деле, пусть в качестве точек взяты точки, являющиеся серединами частичных сегментов:
взяты точки, являющиеся серединами частичных сегментов:

Вычислим значения функции в этих точках:

Составим интегральную сумму:
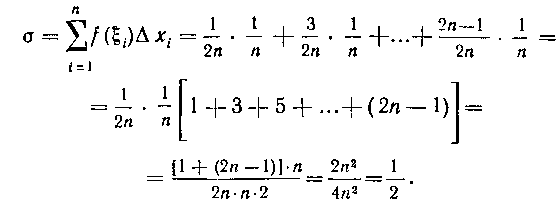
Вычислим предел полученной интегральной суммы при стремлении к нулю наибольшего из частичных сегментов:
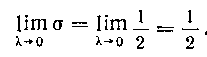
Полученный предел является значением определенного интеграла.

322. Вычислить интеграл:
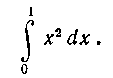
Решение. Разобьем отрезок [О, I] на п равных частей точками
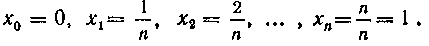
Получим п частичных сегментов:

Длина каждого частичного сегмента равна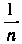 . В качестве точек
. В качестве точек Выберем самые правые точки частичных сегментов:
Выберем самые правые точки частичных сегментов:

Вычислим значения функции В этих точках:
В этих точках:
Составим интегральную сумму:

Вычислим предел интегральной суммы при Таким образом,
Таким образом,
323. Вычислить интеграл:
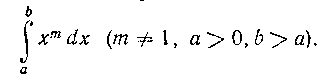
Решение. Разсбьем сегмент \ач bI течками деления
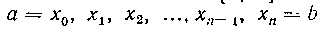
и потребуем, чтобы эти точки составляли геометрическую прогрессию

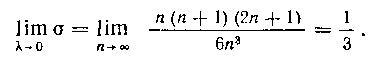

Знаменатель прогрессии

Длины частичных сегментов будут:
 или
или
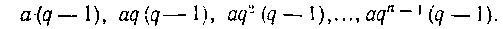
В качестве точек Ii выберем самые правые точки
частичных сегментов:
Составим интегральную сумму:

Вычислим предел интегральной суммы при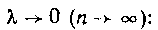
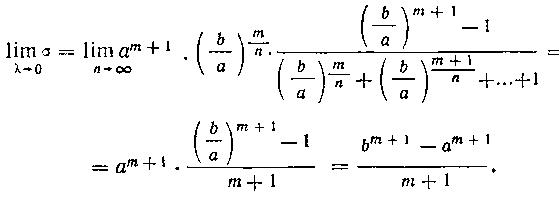
Таким образом,
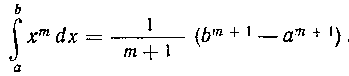

Вычислим значения функции. _ В этих точках:
В этих точках:
324. Вычислить интеграл:

Решение. Для удобства вычислений разобьем сегмент [I, 2] точками На п частичных сегментов так, "чтобы точки деления составляли геометрическую прогрессию. Обозначим через q знаменатель шэогвессии, тогда точки разбиения будут
На п частичных сегментов так, "чтобы точки деления составляли геометрическую прогрессию. Обозначим через q знаменатель шэогвессии, тогда точки разбиения будут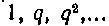
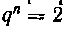 И, следовательно,
И, следовательно,

Длины частичных сегментов будут:
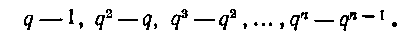
В качестве точек Выберем самые правые точки
Выберем самые правые точки
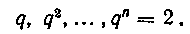
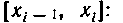
Вычислим значения функции В этих точках:
В этих точках:

Составим интегральную сумму:
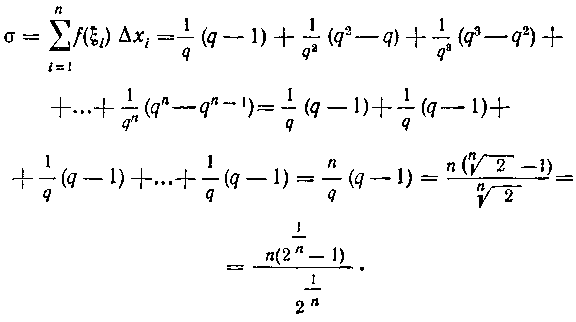
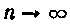
Вычислим предел интегральной суммы при

Заменим переменную под знаком предела, положив
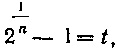 Тогда
Тогда И, следовательно, при п-*оо
И, следовательно, при п-*оо
будет Так как
Так как Откуда
Откуда

поскольку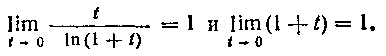
Таким образом,


325. Вычислить интеграл разбивая сегмент 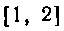 На равные части.
На равные части.
326. Вычислить интеграл Разбивая сегмент
Разбивая сегмент  На равные части.
На равные части.
327. Вычислить интеграл , разбивая сегмент
, разбивая сегмент
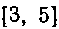 Так, чтобы точки деления сегмента составляли геометрическую прогрессию.
Так, чтобы точки деления сегмента составляли геометрическую прогрессию.
328. Вычислить интеграл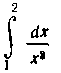 , разбивая сегмент
, разбивая сегмент
 Так, чтобы точки деления сегмента составляли геометрическую прогрессию.
Так, чтобы точки деления сегмента составляли геометрическую прогрессию.
329. Вычислить Разбивая сегмент
Разбивая сегмент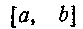
так, чтобы точки деления сегмента составляли геометрическую прогрессию.
330. Вычислить интеграл , разбивая сегмент
, разбивая сегмент
так, чтобы точки деления сегмента составляли геометрическую прогрессию.
2. Вычисление определенных интегралов из геометрических соображений. Предварительно изучите по учебнику Г. М. Фихтенгольца главу X, п° 156 и главу XI, п° 175.
Как известно из теоретического курса (п° 175), определенный интеграл dx численно равен площади кри

волинейнойтрапеции аАВЬ (рис. I), ограниченной сверху кривой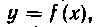 Ординатами х = а и х = Ь и отрез
Ординатами х = а и х = Ь и отрез
ком оси абсцисс.
331. Используя геометрические соображения, вычислить:


Решение. Обозначив подынтегральную функцию через у, получим: это — окружность радиуса а с центром в начале координат (рис. 2). Подынтегральная функция представляет собой верхнюю половину этой окружности. Так как площадь круга равна
это — окружность радиуса а с центром в начале координат (рис. 2). Подынтегральная функция представляет собой верхнюю половину этой окружности. Так как площадь круга равна То
То

332. Используя геометрические соображения, вычислить:

Решение. Обозначим подынтегральную функцию через у. Кривая у = sin х изображена на рисунке 3. Разобьем
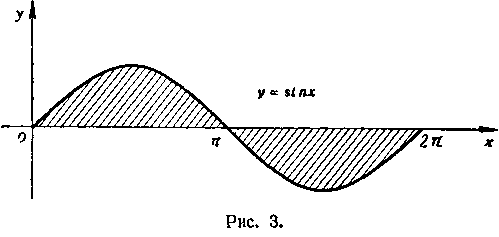
промежуток интегрирования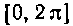 На два сегмента
На два сегмента И
И
 . Из рисунка 3 видно, что кривая
. Из рисунка 3 видно, что кривая Располо
Располо
жена на сегменте [0, я] над осью Ох, а на сегменте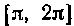 под осью Ох. Обозначим площади, образуемые данной кривойс осью Ox на этих участках, соответственно через S1 и.
под осью Ох. Обозначим площади, образуемые данной кривойс осью Ox на этих участках, соответственно через S1 и.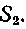 Как видно из рисунка 3, численные значения этих площадей равны, но имеют противоположные знаки
Как видно из рисунка 3, численные значения этих площадей равны, но имеют противоположные знаки
 . Отсюда следует, что
. Отсюда следует, что

Используя геометрические соображения, вычислить следующие интегралы:
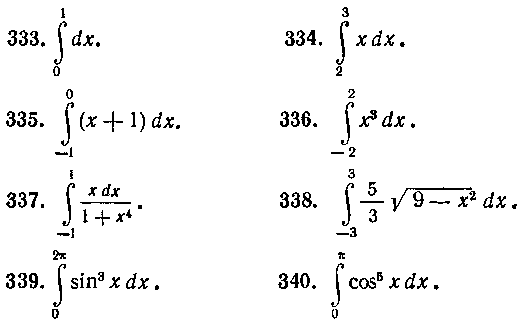
3. Основные свойства определенных интегралов. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XI, п° 180— 183.
341. Оценить интеграл:
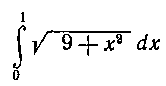
Решение. Так как в данной задаче 0 <х < I, следовательно, 0 < X2 < I, то для подынтегральной функции справедливы неравенства:
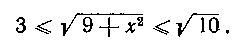
Воспользовавшись теперь свойством 8 определенного интеграла (см. учебник, п° 182), находим оценку заданного интеграла:
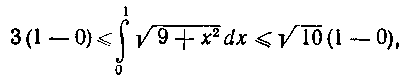
или окончательно

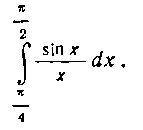
Решение. На заданном отрезке подынтегральная функция монотонно убывает. В самом деле, если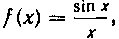 То
То
всюду на отрезке Производная
Производная
По определению монотонно убывающей функции из неравенств следуют неравенства

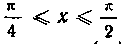
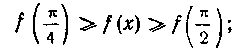
следовательно, по указанному выше свойству определенного интеграла
или
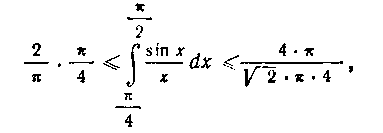
откуда

В задачах 343—346 оценить интегралы.

347. Найти среднее значение функции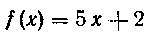 на отрезке
на отрезке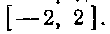
Решение. Средним значением функции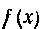 На отрезке
На отрезке Называется число
Называется число

В данном случае
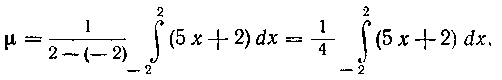
Используя свойства 3 и 4 определенного интеграла (см. учебник, п°181), получим:


Из геометрических соображений ясно, что а
а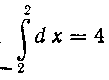 (см. рис. 4). Следовательно,
(см. рис. 4). Следовательно,
348. He вычисляя значений интегралов установить, величина какого из них больше.
установить, величина какого из них больше.

Решение. Как известно (п° 182),если функции и g(x) интегрируемы на сегменте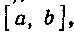 Где
Где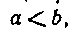 И
И
 На этом сегменте, то
На этом сегменте, то
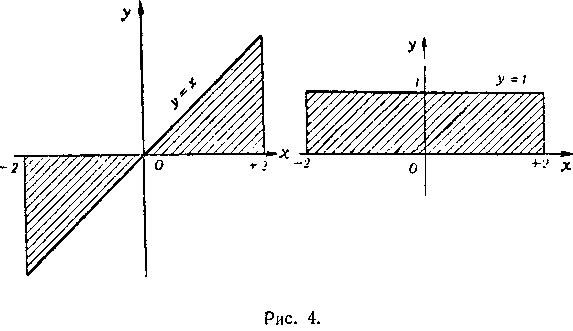
Обозначим через f(x) подынтегральную функцию первого интеграла, т. е. f(x) — x, а через g (х) подынтегральную функцию второго интеграла, т. е.
Функции f(x) и g (х) непрерывны на сегментеГО. 11, следовательно, и интегрируемы на нем, и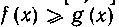 (знак равенства реализуется на концах сегмента). Отсюда следует, что
(знак равенства реализуется на концах сегмента). Отсюда следует, что
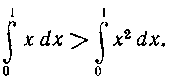

349. Доказать неравенство:


Решение. Рассмотрим интегралы, Обо
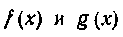
значим через соответствующие подынтеграль-
ные функции, т. е.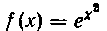 И
И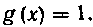 Этифункции
Этифункции
непрерывны на сегменте [О, I], причем . Из
. Из
геометрических соображений ясно, чтс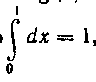 , следова
, следова
тельно,
Левая часть неравенств доказана. Рассмотрим интегралы 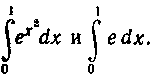 Обозначим подынтегральные функции этих
Обозначим подынтегральные функции этих
интегралов соответственно через г И
И
Эти функции непрерывны на сегменте [О, I], причем
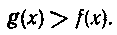 Следовательно,
Следовательно, Правая
Правая
часть неравенств доказана. Таким образом, неравенства доказаны полностью.
350. Найти среднее значение функции / (х) на указанных сегментах:
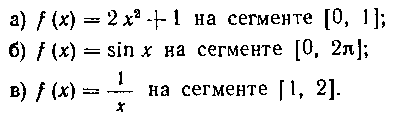
351. He вычисляя интегралов, установить, величина какого из указанных ниже интегралов больше:


352. Доказать неравенства:
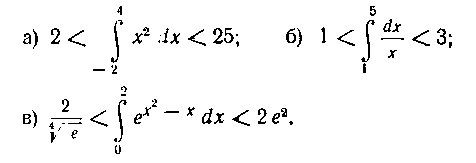
353. Найти производную функции:

Решение. Из теоретического курса известно, что производная интеграла с постоянным нижним пределом и переменным верхним пределом равна подынтегральной функции при значении ее аргумента, равном верхнему пределу. Пользуясь свойствами определенного интеграла, преобразуем данный интеграл:

Найдем теперь Производную заданной функции, пользуясь правилом дифференцирования сложной функции

354. Функция задана параметрически:

Найти производную
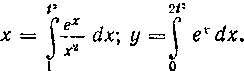
Решение. Если функция задана параметрически уравнениями

то

Найдем предварительно


Таким образом,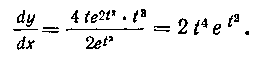
В задачах 355 — 356 найти производные следующих функций:
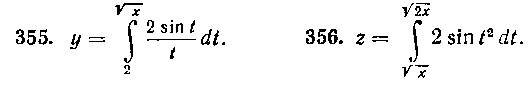
357. Кривая задана уравнениями в параметрической форме:

Определить величину угла, образованного касательной к этой кривой с положительным направлением оси Ох.
358. Кривая задана уравнением:

Определить величину угла, образованного касательной к этой кривой в точкес положительным направ
лением оси Ох.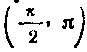
359. Найти точки экстремума функции

в области х > 0.
360. Найти точки экстремума и точки перегиба для функции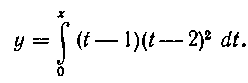
| < Предыдущая | Следующая > |
|---|