2.I. Интегрирование рациональных функций
Предварительно изучите по учебнику Г. М. Фихтен-гольца главу X, п° 164—167. Перед тем как перейти к решению задач на случай 4, еще раз внимательно разберите решение примера 5 в п° 163 учебника.
При решении задач настоящего параграфа в тех случаях, когда степень многочлена в числителе больше или равна степени многочлена в знаменателе, не забывайте предварительно исключить целую часть.
Случай I. В разложение знаменателя рациональной функции входят только множители первой степени и ни один из них не повторяется.
179. Найти интеграл:
Решение. Так как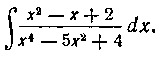
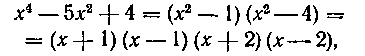
то подынтегральную функцию мы разложим на такие простейшие дроби:
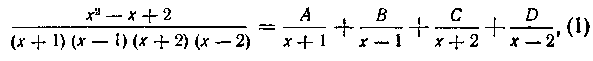
где постоянные A9 By С, D найдем следующим образом с помощью метода неопределенных коэффициентов (как мы поступали выше при решении задачи 132).
Приводим равенство (I) к общему знаменателю д последний отбрасываем:
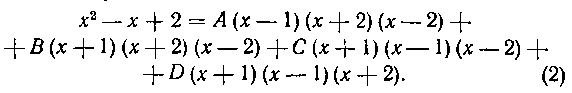
Равенство (2) справедливо при любых значениях х. Поэтому выбираем теперь четыре*) таких значения х, каждое из которых обратило бы в нуль какой-нибудь из сомножителей в правой части (2). В нашей задаче такими значениями являются: х = — I, X=I9 х = — 2, х = 2. Подставив поочередно эти значения в равенство (2), получим:
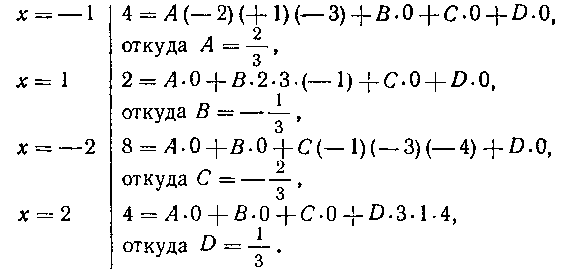
Таким образом, мы получили следующее разложение рациональной дроби на простейшие:
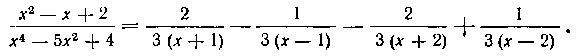
Интегрируя, находим:
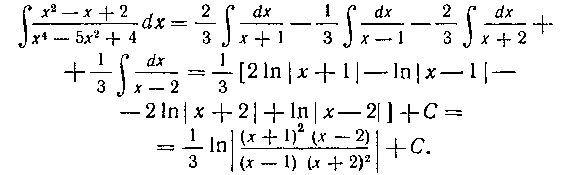
Четыре значения Jr потому, что нам надо найти четыре неопределенных коэффициента, число которых, всегда равно степени знаменателя.
Разумеется, мы могли бы искать неопределенные коэффициенты А, В, С, D и так, как мы это делали при решении задачи 131. Однако в случае I это немного усложняет отыскание указанных коэффициентов.
180. Найти интеграл:
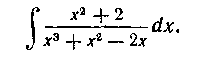
Решение. Так как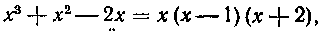 то аналогично решению предыдущей задачи пишем следующее разложение подынтегральной функции:
то аналогично решению предыдущей задачи пишем следующее разложение подынтегральной функции:
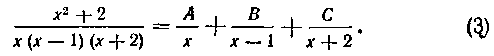
Далее имеем:
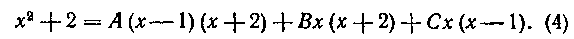
Замечание. Обращаем внимание читателя на то, что ни в предыдущей задаче, ни в настоящей мы намеренно не раскрываем скобок в правой части равенства (4), так как это привело бы не к упрощению, а, наоборот, к некоторому усложнению подсчета коэффициентов. В задачах, относящихся к случаю I, так всегда рекомендуем поступать.
Находим теперь значения равенства (4) при х = 0,
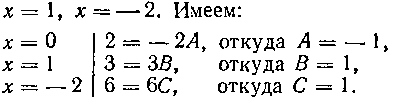
Теперь разложение (3) мы можем переписать в виде
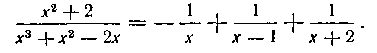
Подставляя полученное выражение в заданный интеграл и производя почленное интегрирование, получим:
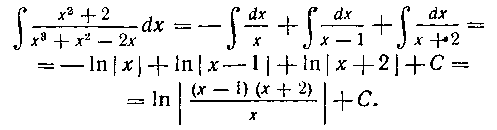
Случай 2. В разложение знаменателя рациональной функции входят только множители первой степени и некоторые из них повторяются.
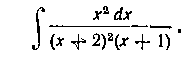
Решение. Знаменатель подынтегральной дроби содержит однократный множитель х - j-1 и двукратный множитель x-j-2, поэтому в данном случае получим следующее разложение на простейшие дробш
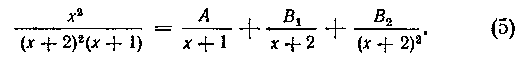
Приводим теперь к общему знаменателю и отбрасываем его. Получим тождество:
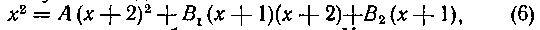
справедливое при любых значениях х. Мы можем здесь назвать лишь два значения х, обращающие в нуль какие-нибудь из слагаемых в равенстве (6), это X = — I и х=—2; однако нам надо отыскать три неопределенных коэффициента A, B1, B2, поэтому дадим х еще одно (любое) значение, например х=0. Подставив поочередно эти три значения в равенстве (6), получим:
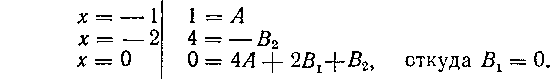
Итак, имеем:
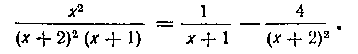
Следовательно, искомый интеграл равен:
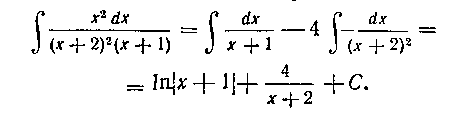
182. Найти интеграл:
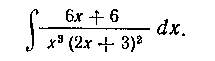
Решение. Для заданной подынтегральной дроби разложение будет иметь вид:
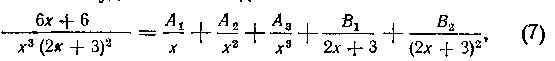
так как в знаменателе множитель х повторяется трижды, а мн<*житель 2х - f - 3 повторяется дважды. Приводя к общему знаменателю, получим:
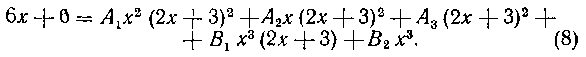
При необходимости определить пять коэффициентов Av A a, A3t Bv B2 мы здесь можем назвать лишь два значения , которые обращают в нуль
, которые обращают в нуль
какие-нибудь из слагаемых в правой части равенства (8). Поэтому одновременно воспользуемся здесь и способом, указанным в решении задачи 131, т. е. приравняем в обеих частях тождества (8) коэффициенты при одинаковых степенях х. Так как нам необходимо вычислить пять коэффициентов A19 A29 A^ B19 B29 томы найдем значения тождеств^ (8) при X = 0, при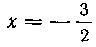 , а также срав-
, а также срав-
глт в обеих частях этого тождества коэффициенты, например, при х\ X2 и х. Получим:
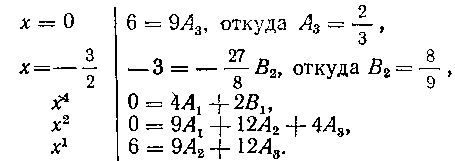
Подставив в последнее уравнение значение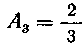 , мы
, мы
найдем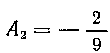 . Затем из предпоследнего уравнения
. Затем из предпоследнего уравнения
найдем A1 = 0 и из первого уравнения находим B1 — 0. Итак, мы получили разложение:
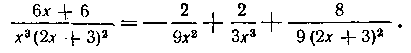
Искомый интеграл теперь легко вычисляем:
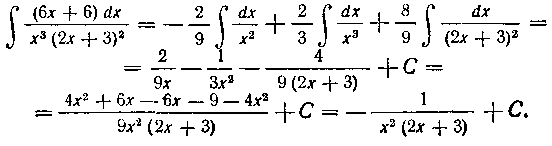
Заданный интеграл можно вычислить иным путем, именно с помощью подстановки
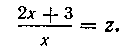
Предлагаем это проделать читателю.
Замечание. Интеграл, рассмотренный в задаче 182, представляет собой частный случай интеграла

в котором пит — целые положительные числа. Интеграл такого типа может быть взят намного проще, чем по общему правилу, с помощью подстановки
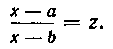
Подробнее смотрите учебник А. Ф. Берманта «Курс математического анализа» (ч. I, изд. 12, Физматгиз, 195в).
Укажем еще один прием вычисления неопределенных коэффициентов, особенно удобный в тех случаях, когда необходимо вычислить лишь какую-то группу коэффициентов. Проиллюстрируем этот прием на примере 182. Для данного в нем интеграла мы представили разложение рациональной дроби в следующем виде:
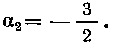
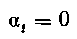 И двукратный корень
И двукратный корень
Займемся сначала отысканием группы неопределенных коэффициентов Alf A2f A3 (все слагаемые в правой части (7'), не содержащие этих коэффициентов, обозначим через /(я))-Для этого сбе части равенства (7') умножим на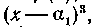 Т. е. в нашем случае просто на л;3, поскольку
Т. е. в нашем случае просто на л;3, поскольку
O1 = O есть трехкратный корень знаменателя дроби. Мы получим следующее тождество:
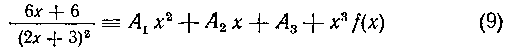
относительно переменного X9 которое, следовательно,
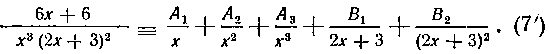
Многочлен в знаменателе дроби имеет трехкратный корень
справедливо при любом значении х. Положив в (9) х = О, получим коэффициент A3:
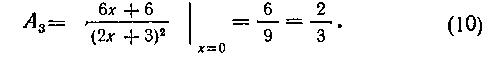
Продифференцируем теперь тождество (9) по х. Мы получим следующее тождество:
Полагая в нем снова х = 0, найдем коэффициент A2:
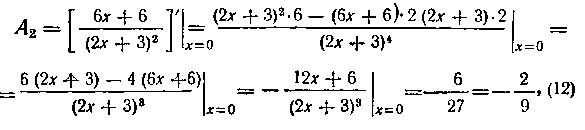
так как все остальные слагаемые обратятся в нуль при х =0. Продифференцировав тождество (11) по х, получим снова тождество:
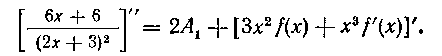
При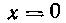 Получим:
Получим:
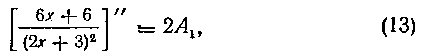
так как все остальные члены правой части обратятся при этом в нуль. Из равенства (13) находим A1:
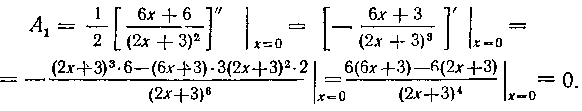
Итак, мы нашли те же значения коэффициентов A19 A2fA3:
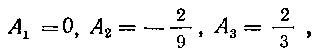
которые ранее в примере 182 (см. стр. 47) были получены другим путем.
Рассуждая точно так же в общем случае, мы легко получим следующие общие формулы для отыскания
неопределенных коэффициентов рациональной дроби. Именно, пусть задана правильная несократимая рациональная дробь вида

где — многочлены. Рассмотрим лишь случай,
— многочлены. Рассмотрим лишь случай,
когда корни многочлена S(x) все вещественны. Тогда, если для многочлена n-й степени £(л:) его разложение на множители имеет вид:
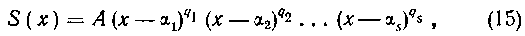
где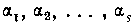 —корни
—корни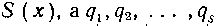 —соответственно их кратности, причем
—соответственно их кратности, причем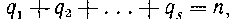 То разложение рациональной дроби (14) на простейшие можно представить в виде:
То разложение рациональной дроби (14) на простейшие можно представить в виде:
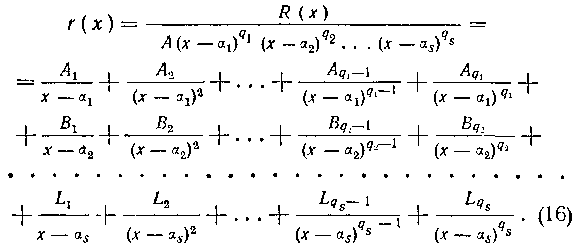
В этом случае неопределенные коэффициенты можно вычислить по следующим формулам:
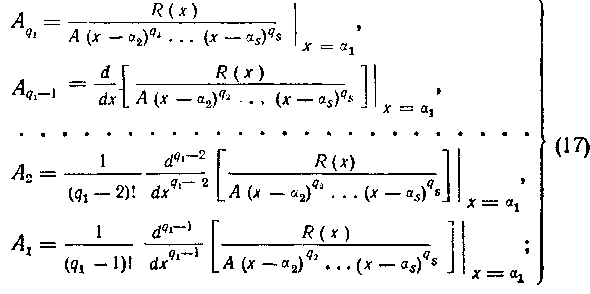
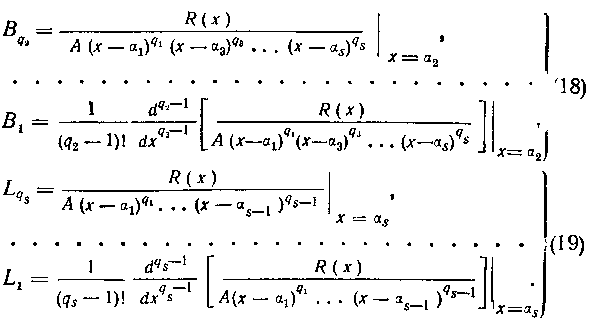
С помощью формул (17)-(19) определим теперь коэффициенты S1 и B2 в разложении (7) для примера 182. Итак, имеем;
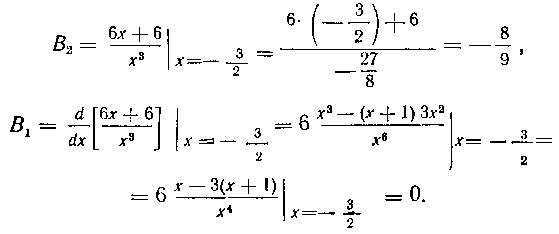
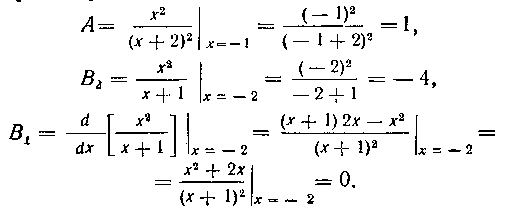
Итак,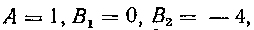 Что совпадает с полученны
Что совпадает с полученны
ми ранее (см. стр. 46) значениями этих коэффициентов. Если многочлен S (х) имеет только простые корни, т. е.
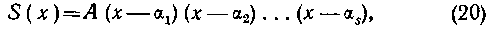
то разложение (16) для рациональной дроби (14) примет более простой вид:
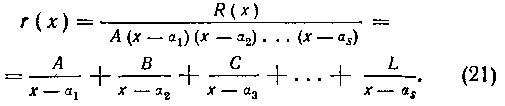
В этом случае для отыскания неопределенных коэффициентов А, В,..., L достаточны будут только первые из формул (17)— (19), которые можно представить в более простом виде. В самом деле, легко видеть, что если аи 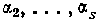 — простые корни многочлена S(x), то
— простые корни многочлена S(x), то
Применим рассмотренный прием к отысканию неопределенных коэффициентов разложения рациональной дроби примера 179. В этом примере (см. стр. 43)
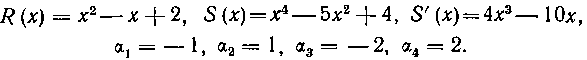
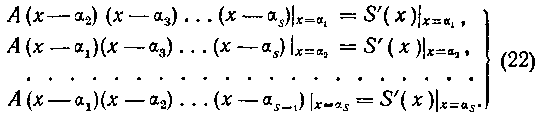
Поэтому в случае простых корней многочлена 5 (х) формулы для определения коэффициентов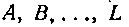 Примут вид:
Примут вид:
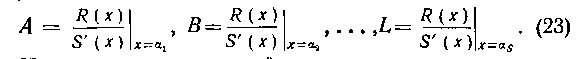
Таким образом, по формулам (23) находим неопределенные коэффициенты в разложении (I):
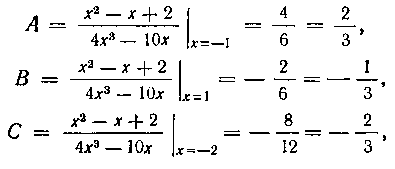
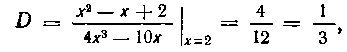
что совпадает с решением примера 179 (см. стр. 44). Рассмотрим разложение рациональной дроби примера 180:
что совпадает со значениями этих коэффициентов, найденными на стр. 45.
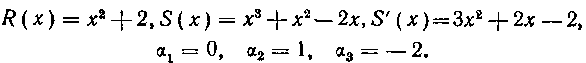
По формулам (23) находим:
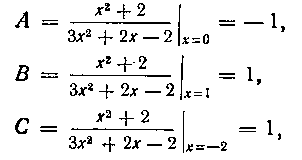
Указанный прием можно применить к отысканию коэффициентов, соответствующих только простым корням многочлена S(я), и в том случае, когда другие его корни кратные или комплексные.
Случай 3. В разложение знаменателя рациональной функции входят множители второй степени (неразложимые на вещественные множители первой степени) и ни один из них не повторяется.
183. Найти интеграл:
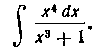
Решение. Предварительно исключаем целую часть рациональной дроби. Имеем:
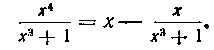
Таким образом, получаем:
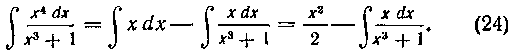 I
I
Далее, так как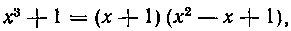 Причем вто
Причем вто
рой сомножитель не разлагается на вещественные множители первой степени, то разложение данной дроби будет иметь вид:
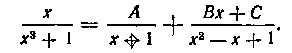
Освобождаемся от знаменателя:
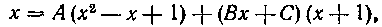
Таким образом, имеем:

Теперь интегрируем:
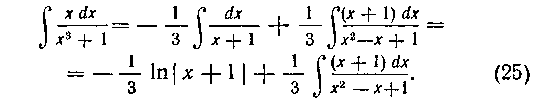
Оставшийся интеграл берем подстановкой (см. решение задачи 130):
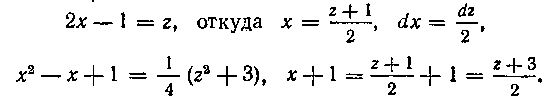
и в полученном тождестве сравниваем коэффициенты при одинаковых степенях х слева и справа:
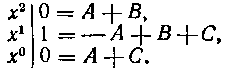
Мы получили систему трех уравнений относительно коэффициентов А. В. С. Решая ее, находим:
Итак,
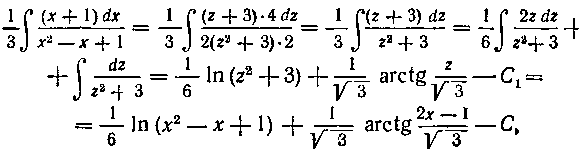
где
Вставляя полученное в равенства (25) и (24), окончательно получим:
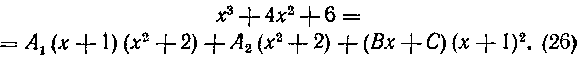
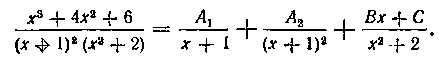
Освобождаясь от знаменателя, получаем тождество:
Приравниваем в нем коэффициенты при одинаковых степенях х слева и справа:
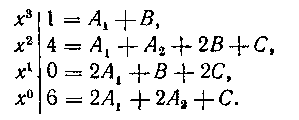
Решая эту систему четырех уравнений, находим:
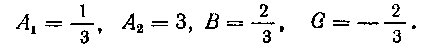
Таким образом, разложение данной рациональной дроби имеет вид:
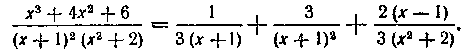
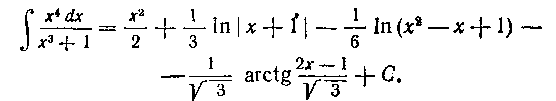
184. Найти интеграл:
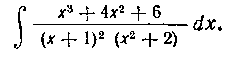
Решерие. Здесь разложение рациональной дроби имеет вид:
Теперь остается проинтегрировать, и мы найдем искомый интеграл:
Случай 4. В разложение знаменателя рациональной функции входят множители второй степени (неразложимые на вещественные множители первой степени) и некоторые из них повторяются.
Здесь речь идет о том, что в разложение знаменателя входят множители вида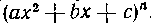 . В § 4 главы I
. В § 4 главы I
мы уже показали, что квадратный трехчлен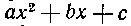 можно привести к каноническому виду
можно привести к каноническому виду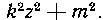 Поэтому
Поэтому
в случае 4 нам обязательно придется иметь дело с интегралами вида

Этот интеграл равен сумме двух интегралов:
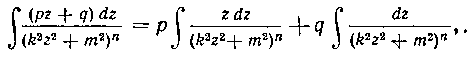
из которых первый берется очень легко:
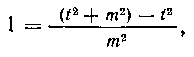
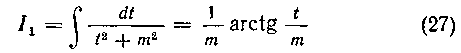

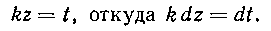

а второй приводится к более простому виду подстановкой В самом деле,
Выведем поэтому формулу приведения для интеграла 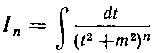 (п—целое положительное).
(п—целое положительное).
При п = I имеем:
(мы берем одно из его значений). Примем теперь, что 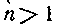 . Заменив в числителе множитель I частным
. Заменив в числителе множитель I частным
мы получим:
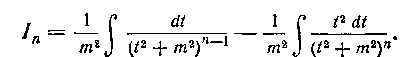
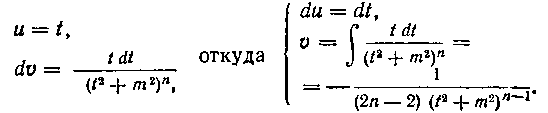
Таким образом,
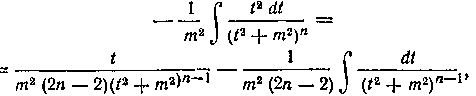
следовательно,
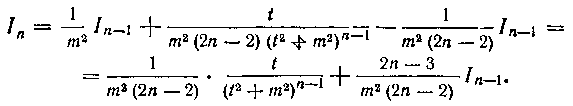
Мы получили, таким образом, формулу приведения»
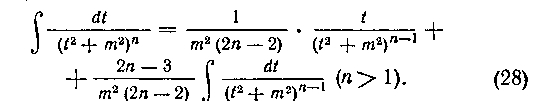
С ее помощью мы можем, например, легко вычислить интеграл
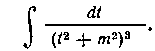
В самом деле, применяя формулу (28), найдем:
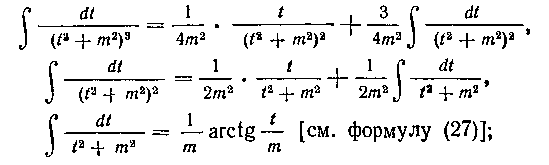
поэтому
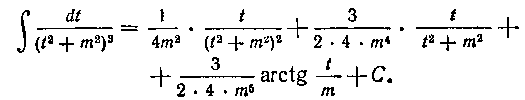
185. Найти интеграл:
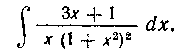
Решение. Разложим данную дробь на простейшие:
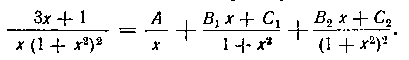
После приведения к общему знаменателю получаем следующее тождество:
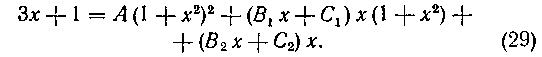
Коэффициенты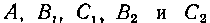 Находим, приравняв
Находим, приравняв
в тождестве (29) коэффициенты при одинаковых степенях х слева и справа. Имеем:
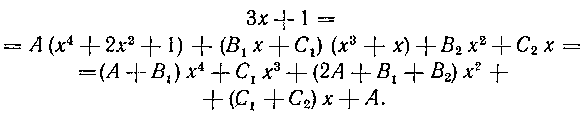
Следовательно, получаем систему:
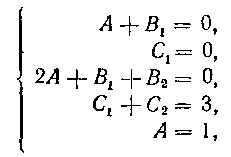
решая которую легко находим:
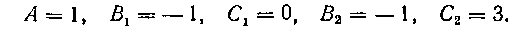
Итак, мы получили разложение:
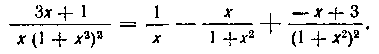
Искомый интеграл, следовательно, равен:
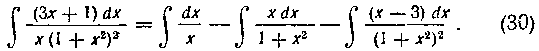
Первые два интеграла в правой части берутся легко (первый из них табличный, а во втором производная знаменателя отличается множителем от числителя):
Мы могли бы воспользоваться здесь и готовой формулой приведения (28).
В задачах 186—207 определить сначала, к какому из разобранных выше 4-х случаев относится интеграл, и вычислить эти интегралы.
Займемся теперь третьим интегралом правой части. Разобьем его на два интеграла и преобразуем так:
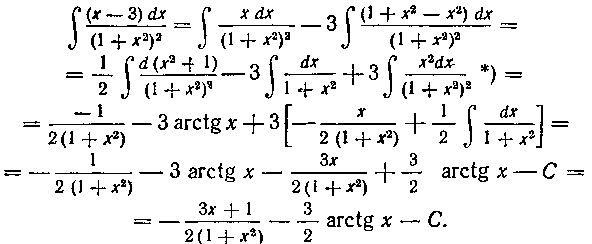
Собирая воедино все интегралы равенства (30), окончательно получим:
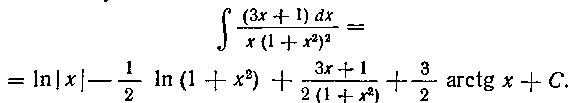
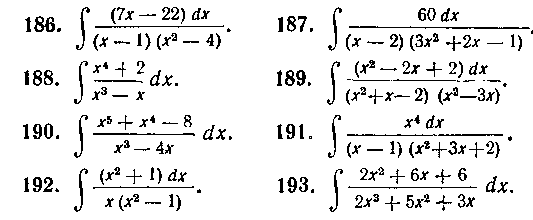
) Последний интеграл берем по частям, полагая
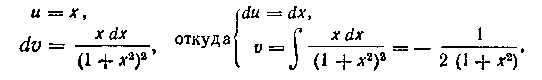
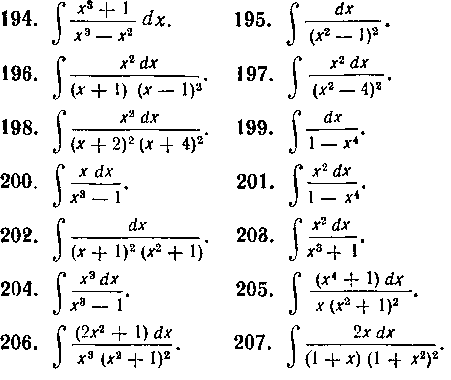
| < Предыдущая | Следующая > |
|---|