2.5. Интегрирование выражений, содержащих тригонометрические функции
Предварительно изучите по учебнику Г. М. Фихтен-гольца главу X, п° 159 (примеры 5, 8), 161 (примеры 3, 46), 171. Особенно внимательно изучите п° 171,
Рассмотрим сначала несколько задач, для решения которых не потребуется никаких дополнительных теоретических сведений, кроме тех, которые были даны в § I и 2 главы I.
241. Найти интеграл:

Решение. Преобразуем подынтегральную функцию, используя равенства
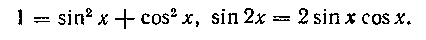
Получим:

Было быгрубой ошибкой здесь принять, что
 Это было бы верно лишь при
Это было бы верно лишь при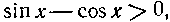 В то времякак при
В то времякак при
должно быть
По определению абсолютной величины имеем:
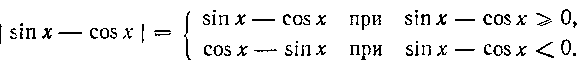
Итак, окончательно имеем:

242. Найти интеграл:
Решение. Множитель sinxcosxdx наводит нас на мысль выбрать подстановку

Решение. Если множитель sinx подвести под знак дифференциала (см. формулу 7 из табл. 2), то сразу напрашивается подстановка cos х = t. Отсюда —sin х dx ~ = dt> и мы получаем:

243. Найти интеграл:


В этом случае имеем:
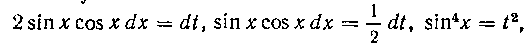
Мы здесь исключили целую часть из подынтегральной дроби; см. решение задачи 4.

Рассмотрим теперь интегралы вида

считая, что т и п—целые положительные числа. Эти интегралы берутся с помощью следующих известных из тригонометрии преобразований:
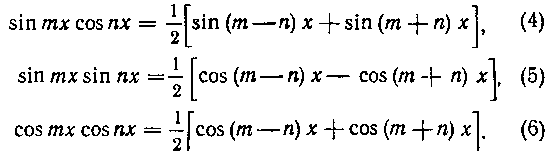
244. Найти интеграл:
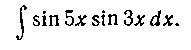
Решение. Воспользовавшись формулой (5), а затем формулой 5 из таблицы I, получим:

245. Найти интеграл:
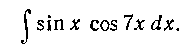
Решение. На основании формулы (4) и формулы б из таблицы I имеем:

72

246. Найти интеграл:

Решение. По формуле (6) получим последовательно:
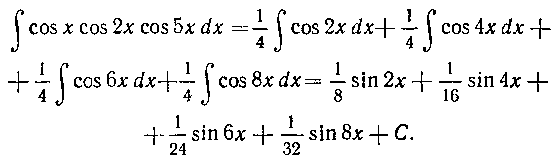


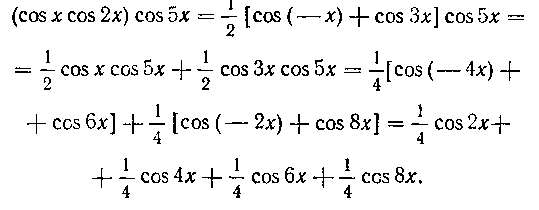
Таким образом,
247. Найдем теперь в общем виде интегралы (I) — (3) с помощью формул (4) — (6).
На основании формулы (4) находим:
Если же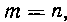 , то формула (4) принимает вид:
, то формула (4) принимает вид:
поэтому
Пользуясь формулой (5), получим:


Если же т = п, то формула (5) принимает вид:  поэтому
поэтому
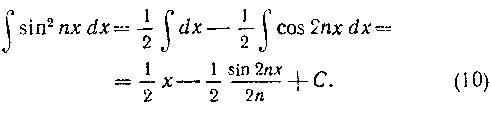
На основании формулы (6) находим:
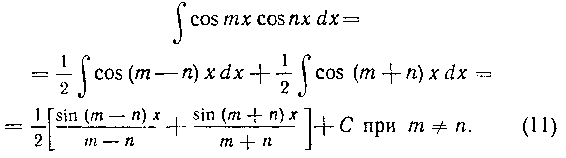
Если же т = п, то формула (6) принимает вид: поэтому

Формулы (7) — (12) нам пригодятся в дальнейшем. Поэтому для удобства пользования соберем их вместе:
74

Интегралы вида
где —рациональная функция от sin л: и cosx,
—рациональная функция от sin л: и cosx,
преобразуются в интегралы от рациональной функции подстановкой

Для этого с помощью равенства (14) выражаем sin х

через t, а также dx через / и dt:

Подстановка (14) называется универсальной. Она применяется, например, при вычислении интегралов вида
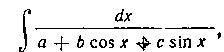
которые с помощью этой подстановки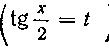 J
J
приво
дятся к интегралам вида

подробно рассмотренным нами в § 4 главы I.
Рассмотрим несколько задач, при решении которых применяется универсальная подстановка.
248. Найти интеграл:
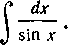
Решение. Применяем подстановку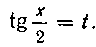 На ос
На ос
новании формул (15) имеем:
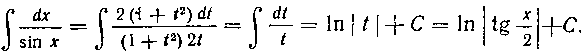
Чтобы обойтись без предварительного запоминания формул (15), рекомендуем поступать так: сначала воспользоваться более простой формулой

затем разделить числитель и знаменатель на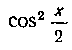 , под
, под
вести под дифференциал множитель - по формуле
- по формуле
8 из таблицы 2 и только после этого применить подстановку
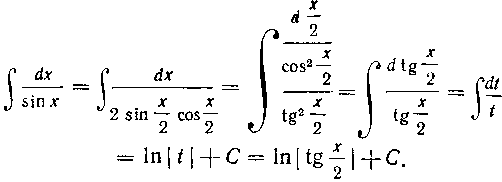
Покажем еще один способ отыскания интеграла задачи 248. Имеем:

Мы воспользовались тождеством , раз
, раз
делили почленно числитель на знаменатель и подвели множитель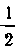 Под дифференциал. Используя теперь реше-
Под дифференциал. Используя теперь реше-
ние задачи 9 и ответ к задаче 42, получим:
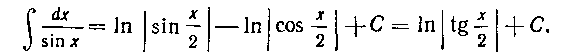
249. Найти интеграл: Решение. Так как
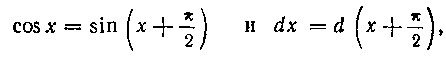
то, применяя подстановку Получим:
Получим:

250. Найти интеграл:

Решение. Воспользуемся тем, что


затем разделим числитель и знаменатель на И возьмем подстановку
И возьмем подстановку
Получим:
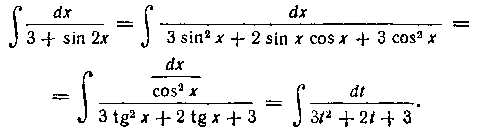
Далее приводим квадратный трехчлен к каноническому виду и берем интеграл (см. § 4, гл. I):

251. Найти интеграл:

Решение. Воспользуемся тем, что
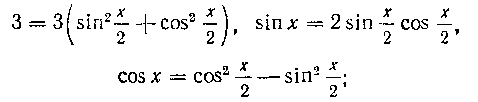
разделим затем числитель и знаменатель наи вос
пользуемся подстановкой

Получим:

Универсальная подстановка часто приводит к сложным выкладкам, поэтому ее следует применять лишь в тех случаях, когда невозможно найти более легкий способ вычисления интеграла. Рассмотрим несколько видов интегралов от тригонометрических функций, которые можно взять проще с помощью других подстановок.
К интегралам вида
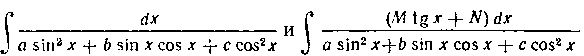
применяется подстановка

с помощью которой они приводятся к интегралам вида
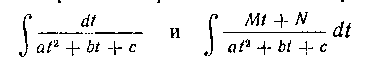
(см. учебник, § 4, гл. I). Рассмотрим соответствующие задачи.
252. Найти интеграл:

Решение. Применяем подстановку
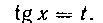
Затем делим числитель и знаменатель на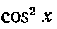 И вводим
И вводим
под знак дифференциала множитель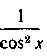 (см. формулу
(см. формулу
7 из табл. I). Мы получим:

(Cm. решение задачи 7.)
253. Найти интеграл:

Решение. Поступаем аналогично решению задачи 252:

Мы здесь взяли подстановку _ И воспользовались формулой 12 из таблицы I.
И воспользовались формулой 12 из таблицы I.
254. Найти интеграл:
Решение. Поступая аналогично решению задачи 252, мы и здесь устанавливаем полезность подстановки

В самом деле, имеем:
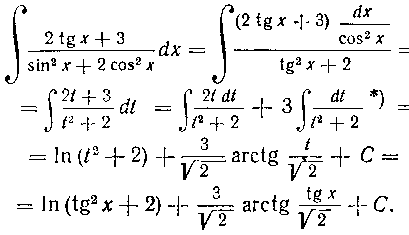
Подстановка tgx = t применяется также к интегралам
вида**)
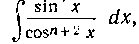
255. Найти интеграл: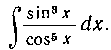
п — целое положительное число.
Решение. Перепишем данный интеграл в виде
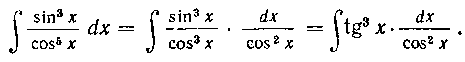
*) Здесь в первом интеграле числитель равен производной знаменателя (см. решение задачи 9); второй интеграл—табличный (см. формулу 9 из табл. I).
**) Аналогично подстановка ctg х = 4 применяется к интегралам 
Применяем подстановку  Имеем:
Имеем:

Рассмотрим теперь интегралы вида

где п — целое положительное число. Рассмотрим сначала случай, когда п — нечетное число.
256. Найти интеграл:

Решение. Отделяем множитель cos* и подводим его под знак дифференциала, а оставшийся множитель cos2* заменяем по формуле Затем
Затем
применяем подстановку
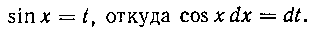
В результате будем иметь:
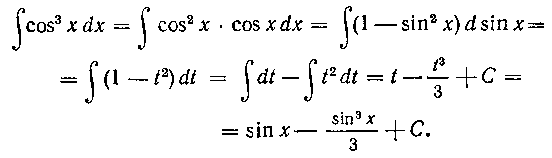
257. Найти интеграл:

Решение. Имеем:

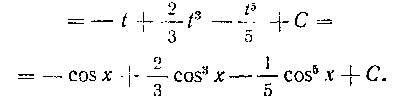
Мы здесь подвели под знак дифференциала множитель sin х и применили подстановку
Рассмотрим теперь случай, когда п — четное число.
258. Найти интегралы:

Решение. Воспользуемся формулами

Заданные интегралы примут вид:

259. Найти интеграл:

Решение. Воспользовавшись формулой
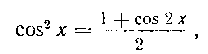
получим:
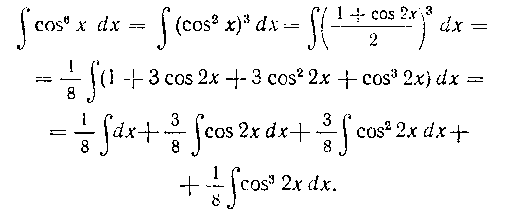
Здесь первый и второй интегралы берутся непосредственно

Рассмотрим подробнее третий и четвертый интегралы. В третьем интеграле, воспользовавшись еще раз указанной формулой, будем иметь:
Поэтому

С четвертым интегралом поступаем, как в случае нечетного показателя степени. Получим:

Мы подвели здесь cos 2х под знак дифференциала

и затем применили подстановку  Окончательно получим:
Окончательно получим:
Интегралы вида


можно вычислить и иным путем. Покажем это и выведем для них так называемые формулы приведений, которые пригодятся читателю значительно позднее.
Итак, пусть дан интеграл
 (п—целое).
(п—целое).
Примем пока, что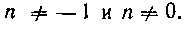 Имеем:
Имеем:

поэтому

откуда после приведения подобных членов будем иметь:

Итак, окончательно получаем:
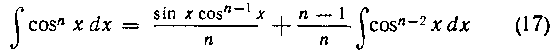
Второй интеграл правой части возьмем по частям, положив в нем

Таким образом,
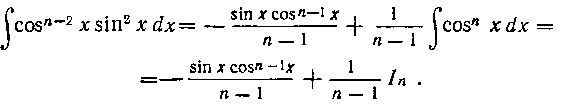
Подставив этот результат в равенство (16), получим:

в предположении, что пф 0.
Заметим, что формулой (17) полезно пользоваться при п положительных (п > 0).
Применение формулы приведения (17) дает возможность значительно быстрее получить ответ. Решим с ее помощью задачу 259. Имеем:

следовательно,

Формулу приведения для п отрицательных (п < 0) мы легко выведем из равенства (17), если перепишем его в виде

и положим в нем

Тогда получим:

Следовательно,

Для k = I смотрите решение задачи 249.
260. Найти интеграл:

Решение. По формуле (18) имеем: (см. решение задачи 249).

Предлагаем читателю совершенно аналогично вьшести самостоятельно следующие формулы приведения:

Cm. также решение задачи 414.
Интегралы вида

где по крайней мере одно из чисел т, п —нечетное, берутся следующим образом.
281. Найти интеграл:
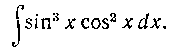
Решение. Мы имеем здесь нечетную степень синуса. Поэтому применяем подстановку cos* = ty и подводим под знак дифференциала множитель sin х. Имеем:

282. Найти интеграл:
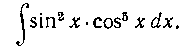
Решение. Здесь мы подводим под знак дифференциала множитель cos х и применяем подстановку  Имеем:
Имеем:
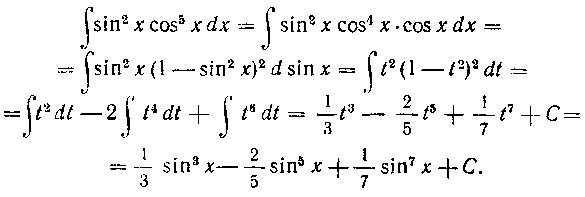
Примечание. Если же т и п — оба четные, то для вычисления интеграла вида (21) удо5но воспользоваться формулами, приведенными в решении задачи 258, а также формулой

Рассмотрим, наконец, интегралы вида

где п — целое положительное.
При п = I мы имеем интегралы:

второй из них вычислен нами раньше (см. задачу 9), первый вычисляется аналогично. Поэтому положим, что п > I. При вычислении интегралов указанного вида выделяют обычно множитель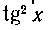 (или
(или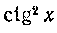 ) и заменяют его по формуле
) и заменяют его по формуле

Читателю станет это яснее при разборе решений следующих задач.
283. Найти интегралы:
Решение. Воспользовавшись формулами (22), получим:

(мы воспользовались здесь формулами 7 и 8 таблицы I).
284. Найти интеграл:
Решение. Имеем:

Теперь в первом полученном интеграле подводим множитель -под знак дифференциала (см. формулу 9
-под знак дифференциала (см. формулу 9
таблицы 2), а во втором снова выделяем множитель Мы получим:
Мы получим:
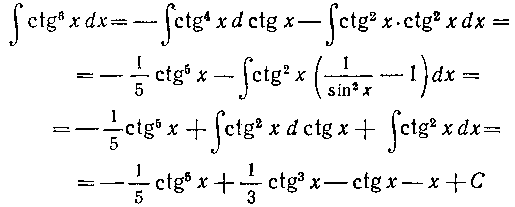
(мы воспользовались здесь равенством (23).
265. Найти интеграл:

Решение. Имеем:

так как

В задачах 266—300 вычислить данные интегралы.
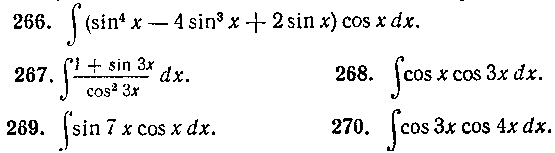
Указание. В задачах 273 и 274 воспользуйтесь формулами.
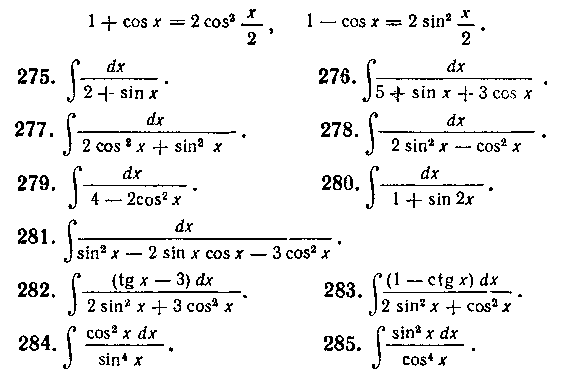
Указание. В задачах 275 и 276 примените подстановку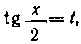
а в задачах 277—283—подстановку В задачах 275, 276,
В задачах 275, 276,
279, 280 свободные члены в знаменателяхпредварительно умножьте на тригонометрическую единицу , Задачи 284 и 285
, Задачи 284 и 285
решаются так же, как задача 255.

Дополнительные задачи к главе I!

Определенный интеграл
ГЛАВА III
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ § I.
| < Предыдущая | Следующая > |
|---|